题目
设严格单调函数y=f(x)有二阶连续导数,其反函数为x=varphi (y),且f(1)=1,(f)'(1)=2,(f)^''(1)=3,则(varphi )^''(1)= .
设严格单调函数$y=f\left(x\right)$有二阶连续导数,其反函数为$x=\varphi \left(y\right)$,且$f\left(1\right)=1$,${f}'\left(1\right)=2$,${f}^{''}\left(1\right)=3$,则${\varphi }^{''}\left(1\right)=$ .
题目解答
答案
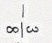
解析
步骤 1:确定反函数的导数
由于$x=\varphi \left(y\right)$是$y=f\left(x\right)$的反函数,根据反函数的导数关系,我们有${\varphi }^{'}\left(y\right)=\dfrac {1} {{f}^{'}\left(x\right)}$。由于$f\left(1\right)=1$,则$\varphi \left(1\right)=1$,因此${\varphi }^{'}\left(1\right)=\dfrac {1} {{f}^{'}\left(1\right)}=\dfrac {1} {2}$。
步骤 2:确定反函数的二阶导数
根据反函数的二阶导数关系,我们有${\varphi }^{''}\left(y\right)=-\dfrac {{f}^{''}\left(x\right)} {{\left({f}^{'}\left(x\right)\right)}^{3}}$。由于$f\left(1\right)=1$,则$\varphi \left(1\right)=1$,因此${\varphi }^{''}\left(1\right)=-\dfrac {{f}^{''}\left(1\right)} {{\left({f}^{'}\left(1\right)\right)}^{3}}=-\dfrac {3} {{2}^{3}}=-\dfrac {3} {8}$。
由于$x=\varphi \left(y\right)$是$y=f\left(x\right)$的反函数,根据反函数的导数关系,我们有${\varphi }^{'}\left(y\right)=\dfrac {1} {{f}^{'}\left(x\right)}$。由于$f\left(1\right)=1$,则$\varphi \left(1\right)=1$,因此${\varphi }^{'}\left(1\right)=\dfrac {1} {{f}^{'}\left(1\right)}=\dfrac {1} {2}$。
步骤 2:确定反函数的二阶导数
根据反函数的二阶导数关系,我们有${\varphi }^{''}\left(y\right)=-\dfrac {{f}^{''}\left(x\right)} {{\left({f}^{'}\left(x\right)\right)}^{3}}$。由于$f\left(1\right)=1$,则$\varphi \left(1\right)=1$,因此${\varphi }^{''}\left(1\right)=-\dfrac {{f}^{''}\left(1\right)} {{\left({f}^{'}\left(1\right)\right)}^{3}}=-\dfrac {3} {{2}^{3}}=-\dfrac {3} {8}$。