题目
解不等式(x-1)/(3)-(x+4)/(2)>-2,并把解集表示在数轴上.
解不等式$\frac{x-1}{3}$-$\frac{x+4}{2}$>-2,并把解集表示在数轴上.
题目解答
答案
解:去分母得,2(x-1)-3(x+4)>-12,
去括号得,2x-2-3x-12>-12,
移项得,2x-3x>-12+2+12,
合并同类项得,-x>2,
系数化为1得,x<-2.
在数轴上表示为:
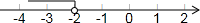 .
.
去括号得,2x-2-3x-12>-12,
移项得,2x-3x>-12+2+12,
合并同类项得,-x>2,
系数化为1得,x<-2.
在数轴上表示为:
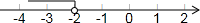 .
.解析
步骤 1:去分母
将不等式两边同时乘以6(即分母的最小公倍数),以消除分母。
步骤 2:去括号
将乘法分配律应用于括号内的表达式。
步骤 3:移项
将所有含x的项移到不等式的一边,将常数项移到另一边。
步骤 4:合并同类项
将同类项合并,简化不等式。
步骤 5:系数化为1
将不等式两边同时除以x的系数,得到x的解集。
步骤 6:表示在数轴上
在数轴上表示解集,用空心圆点表示不包含的端点,用实心圆点表示包含的端点。
将不等式两边同时乘以6(即分母的最小公倍数),以消除分母。
步骤 2:去括号
将乘法分配律应用于括号内的表达式。
步骤 3:移项
将所有含x的项移到不等式的一边,将常数项移到另一边。
步骤 4:合并同类项
将同类项合并,简化不等式。
步骤 5:系数化为1
将不等式两边同时除以x的系数,得到x的解集。
步骤 6:表示在数轴上
在数轴上表示解集,用空心圆点表示不包含的端点,用实心圆点表示包含的端点。