题目
【题目】-|||-计算下列积分:-|||-int dfrac (dxdydz)({(1+x+y+z))^3} ,其中V是由 x+y+z=1 与三个坐标面所围成的区域;

题目解答
答案
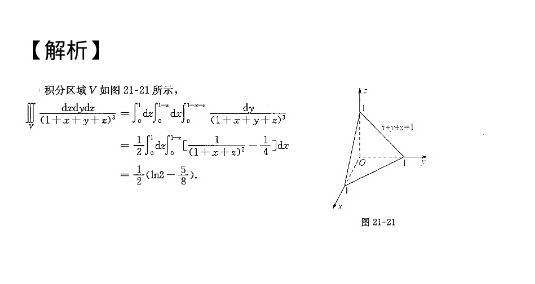
解析
步骤 1:确定积分区域
积分区域V是由平面x+y+z=1与三个坐标面x=0, y=0, z=0所围成的区域。这是一个在第一卦限内的四面体区域。
步骤 2:设置积分的上下限
由于积分区域V是由x+y+z=1与三个坐标面所围成的,因此可以将积分区域V表示为:
$0 \leq x \leq 1$
$0 \leq y \leq 1-x$
$0 \leq z \leq 1-x-y$
步骤 3:计算积分
根据步骤2中的积分上下限,可以将积分写为:
$\int_{0}^{1} \int_{0}^{1-x} \int_{0}^{1-x-y} \dfrac {1}{{(1+x+y+z)}^{3}} dz dy dx$
步骤 4:计算内层积分
首先计算内层积分,即对z的积分:
$\int_{0}^{1-x-y} \dfrac {1}{{(1+x+y+z)}^{3}} dz$
令u=1+x+y+z,则du=dz,当z=0时,u=1+x+y;当z=1-x-y时,u=2。因此,内层积分变为:
$\int_{1+x+y}^{2} \dfrac {1}{u^{3}} du$
$=\dfrac {1}{2}[\dfrac {1}{(1+x+y)^{2}}-\dfrac {1}{4}]$
步骤 5:计算外层积分
将步骤4的结果代入外层积分,得到:
$\int_{0}^{1} \int_{0}^{1-x} \dfrac {1}{2}[\dfrac {1}{(1+x+y)^{2}}-\dfrac {1}{4}] dy dx$
$=\dfrac {1}{2} \int_{0}^{1} [\dfrac {1}{1+x}-\dfrac {1}{4}(1-x)] dx$
$=\dfrac {1}{2}[\ln(1+x)-\dfrac {1}{4}(1-x)]_{0}^{1}$
$=\dfrac {1}{2}(\ln 2-\dfrac {1}{4})$
积分区域V是由平面x+y+z=1与三个坐标面x=0, y=0, z=0所围成的区域。这是一个在第一卦限内的四面体区域。
步骤 2:设置积分的上下限
由于积分区域V是由x+y+z=1与三个坐标面所围成的,因此可以将积分区域V表示为:
$0 \leq x \leq 1$
$0 \leq y \leq 1-x$
$0 \leq z \leq 1-x-y$
步骤 3:计算积分
根据步骤2中的积分上下限,可以将积分写为:
$\int_{0}^{1} \int_{0}^{1-x} \int_{0}^{1-x-y} \dfrac {1}{{(1+x+y+z)}^{3}} dz dy dx$
步骤 4:计算内层积分
首先计算内层积分,即对z的积分:
$\int_{0}^{1-x-y} \dfrac {1}{{(1+x+y+z)}^{3}} dz$
令u=1+x+y+z,则du=dz,当z=0时,u=1+x+y;当z=1-x-y时,u=2。因此,内层积分变为:
$\int_{1+x+y}^{2} \dfrac {1}{u^{3}} du$
$=\dfrac {1}{2}[\dfrac {1}{(1+x+y)^{2}}-\dfrac {1}{4}]$
步骤 5:计算外层积分
将步骤4的结果代入外层积分,得到:
$\int_{0}^{1} \int_{0}^{1-x} \dfrac {1}{2}[\dfrac {1}{(1+x+y)^{2}}-\dfrac {1}{4}] dy dx$
$=\dfrac {1}{2} \int_{0}^{1} [\dfrac {1}{1+x}-\dfrac {1}{4}(1-x)] dx$
$=\dfrac {1}{2}[\ln(1+x)-\dfrac {1}{4}(1-x)]_{0}^{1}$
$=\dfrac {1}{2}(\ln 2-\dfrac {1}{4})$