题目
已知可导函数y=f(x)满足y=f(x),且y=f(x),(1)求函数y=f(x)的表达式;(2)求y=f(x)、y=f(x)及y=f(x)围成的平面图形绕y轴旋转所得旋转体的体积.
已知可导函数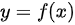 满足
满足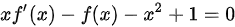 ,且
,且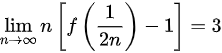 ,
,
(1)求函数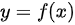 的表达式;
的表达式;
(2)求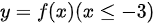 、
、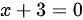 及
及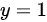 围成的平面图形绕y轴旋转所得旋转体的体积.
围成的平面图形绕y轴旋转所得旋转体的体积.
题目解答
答案
(1)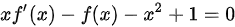 ,则
,则 ,则此方程为一阶线性微分方程,一阶线性微分方程的通解公式为
,则此方程为一阶线性微分方程,一阶线性微分方程的通解公式为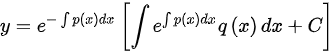 ,其中
,其中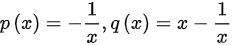 ,则
,则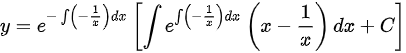
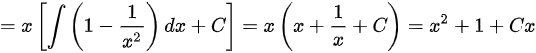 ,
,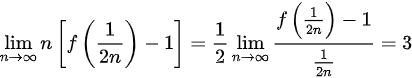 ,则
,则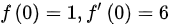 ,则
,则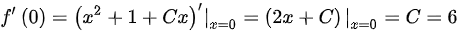 ,满足初始条件的特解为
,满足初始条件的特解为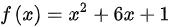 ;(2)
;(2)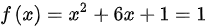 ,则
,则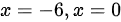 ,则
,则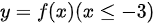 、
、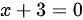 及
及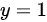 围成的平面图形绕y轴旋转所得旋转体的体积为
围成的平面图形绕y轴旋转所得旋转体的体积为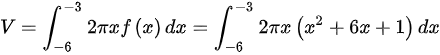
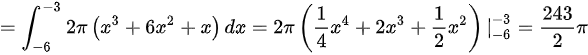 .
.
解析
步骤 1:求解一阶线性微分方程
$xf'(x)-f(x)-{x}^{2}+1=0$,则$f'(x)-\dfrac {1}{x}f(x)=x-\dfrac {1}{x}$,此方程为一阶线性微分方程,一阶线性微分方程的通解公式为$y={e}^{-\int }_{p}(x)dx[ \int {e}^{fp(x)dx}g(x)dx+C] $,其中$p(x)=-\dfrac {1}{x}$,$g(x)=x-\dfrac {1}{x}$,则$y={e}^{-\int }-(1-\dfrac {1}{3})dx[ \int {e}^{f(-\dfrac {1}{2})}x|(x-\dfrac {1}{x})dx+C] $$=x[ 1$ $(1-\dfrac {1}{{x}^{2}})dx+C] =x(x+\dfrac {1}{x}+C)={x}^{2}+1+Cx$,$\lim _{n\rightarrow \infty }n[ f(\dfrac {1}{2n})-1] =\dfrac {1}{2}\lim _{n\rightarrow \infty }\dfrac {f(\dfrac {1}{2n})-1}{\dfrac {1}{2n}}=3$,则f(0)=1,f'(0)=6,则$f'(0)=({x}^{2}+1+{C}_{x})'{x}_{x=0}={(2x+C)}_{x=0}=C=6$,满足初始条件的特解为$f(x)={x}^{2}+6x+1$;
步骤 2:求解旋转体的体积
$f(x)={x}^{2}+6x+1=1$,则$x=-6$,x=0,则$y=f(x)(x\leqslant -3)$、x+3=0及y=1围成的平面图形绕y轴旋转所得旋转体的体积为$v= 2πxf(x)dx= 2πx(x^2+6x+1)dx$=${\int }_{-0}^{-1}2x({x}^{3}+6{x}^{2}+x)dx=2\pi (\dfrac {1}{4}{x}^{3}+2{x}^{8}+\dfrac {1}{2}{x}^{2})-8=\dfrac {248}{2}$ ".
$xf'(x)-f(x)-{x}^{2}+1=0$,则$f'(x)-\dfrac {1}{x}f(x)=x-\dfrac {1}{x}$,此方程为一阶线性微分方程,一阶线性微分方程的通解公式为$y={e}^{-\int }_{p}(x)dx[ \int {e}^{fp(x)dx}g(x)dx+C] $,其中$p(x)=-\dfrac {1}{x}$,$g(x)=x-\dfrac {1}{x}$,则$y={e}^{-\int }-(1-\dfrac {1}{3})dx[ \int {e}^{f(-\dfrac {1}{2})}x|(x-\dfrac {1}{x})dx+C] $$=x[ 1$ $(1-\dfrac {1}{{x}^{2}})dx+C] =x(x+\dfrac {1}{x}+C)={x}^{2}+1+Cx$,$\lim _{n\rightarrow \infty }n[ f(\dfrac {1}{2n})-1] =\dfrac {1}{2}\lim _{n\rightarrow \infty }\dfrac {f(\dfrac {1}{2n})-1}{\dfrac {1}{2n}}=3$,则f(0)=1,f'(0)=6,则$f'(0)=({x}^{2}+1+{C}_{x})'{x}_{x=0}={(2x+C)}_{x=0}=C=6$,满足初始条件的特解为$f(x)={x}^{2}+6x+1$;
步骤 2:求解旋转体的体积
$f(x)={x}^{2}+6x+1=1$,则$x=-6$,x=0,则$y=f(x)(x\leqslant -3)$、x+3=0及y=1围成的平面图形绕y轴旋转所得旋转体的体积为$v= 2πxf(x)dx= 2πx(x^2+6x+1)dx$=${\int }_{-0}^{-1}2x({x}^{3}+6{x}^{2}+x)dx=2\pi (\dfrac {1}{4}{x}^{3}+2{x}^{8}+\dfrac {1}{2}{x}^{2})-8=\dfrac {248}{2}$ ".