题目
若二次型((x)_(1),(x)_(2),(x)_(3))=2({x)_(1)}^2+4({x)_(2)}^2+a({x)_(3)}^2+2b(x)_(1)(x)_(3)经正交变换化为((x)_(1),(x)_(2),(x)_(3))=2({x)_(1)}^2+4({x)_(2)}^2+a({x)_(3)}^2+2b(x)_(1)(x)_(3),则( ).A.((x)_(1),(x)_(2),(x)_(3))=2({x)_(1)}^2+4({x)_(2)}^2+a({x)_(3)}^2+2b(x)_(1)(x)_(3)B.((x)_(1),(x)_(2),(x)_(3))=2({x)_(1)}^2+4({x)_(2)}^2+a({x)_(3)}^2+2b(x)_(1)(x)_(3)C.((x)_(1),(x)_(2),(x)_(3))=2({x)_(1)}^2+4({x)_(2)}^2+a({x)_(3)}^2+2b(x)_(1)(x)_(3)D.((x)_(1),(x)_(2),(x)_(3))=2({x)_(1)}^2+4({x)_(2)}^2+a({x)_(3)}^2+2b(x)_(1)(x)_(3)
若二次型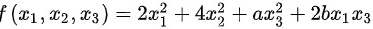 经正交变换化为
经正交变换化为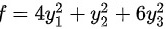 ,则( ).
,则( ).
A.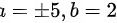
B.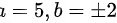
C.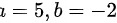
D.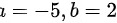
题目解答
答案
由标准形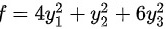 知,二次型矩阵的特征值为
知,二次型矩阵的特征值为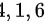 .
.
二次型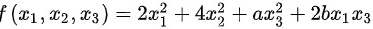 的矩阵为
的矩阵为
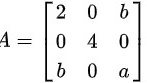 ,由
,由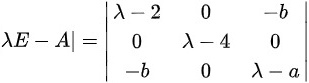
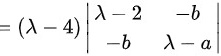
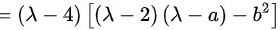
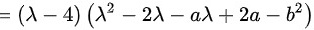
令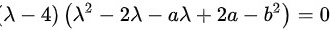 ,得
,得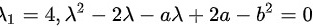 .
.
又已知,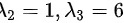
由韦达定理知,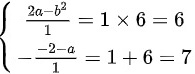
得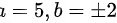 .
.
故此题选B.
解析
步骤 1:确定二次型矩阵的特征值
由标准形$f=4{{y}_{1}}^{2}+{{y}_{2}}^{2}+6{{y}_{3}}^{2}$知,二次型矩阵的特征值为4,1,6.
步骤 2:写出二次型矩阵
二次型$({x}_{1},{x}_{2},{x}_{3})=2{{x}_{1}}^{2}+4{{x}_{2}}^{2}+a{{x}_{3}}^{2}+2b{x}_{1}{x}_{3}$的矩阵为
$20$ ${b}^{-}$ A= $0\quad 4$ 0 $b\quad 0$ a.
步骤 3:计算特征多项式
由$|AE-A|=$ $\left |\begin{matrix} \lambda -2& 0& -b\\ 0& \lambda -4& 0\\ -b& 0& \lambda -a\end{matrix} | \right.$
$=(\lambda -4)$ $\left |\begin{matrix} \lambda -2& -b\\ -b& \lambda -a\end{matrix} | \right.$
$=(\lambda -4)[ (\lambda -2)(\lambda -a)-{b}^{2}] $
$=(\lambda -4)({\lambda }^{2}-2\lambda -a\lambda +2a-{b}^{2})$
步骤 4:求解特征值方程
令$(\lambda -4)({\lambda }^{2}-2\lambda -a\lambda +2a-{b}^{2})=0$,得${\lambda }_{1}=4,$, ${x}^{2}-2\lambda -a\lambda +2a-{b}^{2}=0$.
又已知,${\lambda }_{2}=1$ ${\lambda }_{3}=6$
步骤 5:利用韦达定理求解a和b
由韦达定理知,$\left \{ \begin{matrix} \dfrac {2a-{b}^{2}}{1}=1\times 6=6\\ -\dfrac {-2-a}{1}=1+6=7\end{matrix} \right.$
得$x=5$ $b=\pm 2$.
由标准形$f=4{{y}_{1}}^{2}+{{y}_{2}}^{2}+6{{y}_{3}}^{2}$知,二次型矩阵的特征值为4,1,6.
步骤 2:写出二次型矩阵
二次型$({x}_{1},{x}_{2},{x}_{3})=2{{x}_{1}}^{2}+4{{x}_{2}}^{2}+a{{x}_{3}}^{2}+2b{x}_{1}{x}_{3}$的矩阵为
$20$ ${b}^{-}$ A= $0\quad 4$ 0 $b\quad 0$ a.
步骤 3:计算特征多项式
由$|AE-A|=$ $\left |\begin{matrix} \lambda -2& 0& -b\\ 0& \lambda -4& 0\\ -b& 0& \lambda -a\end{matrix} | \right.$
$=(\lambda -4)$ $\left |\begin{matrix} \lambda -2& -b\\ -b& \lambda -a\end{matrix} | \right.$
$=(\lambda -4)[ (\lambda -2)(\lambda -a)-{b}^{2}] $
$=(\lambda -4)({\lambda }^{2}-2\lambda -a\lambda +2a-{b}^{2})$
步骤 4:求解特征值方程
令$(\lambda -4)({\lambda }^{2}-2\lambda -a\lambda +2a-{b}^{2})=0$,得${\lambda }_{1}=4,$, ${x}^{2}-2\lambda -a\lambda +2a-{b}^{2}=0$.
又已知,${\lambda }_{2}=1$ ${\lambda }_{3}=6$
步骤 5:利用韦达定理求解a和b
由韦达定理知,$\left \{ \begin{matrix} \dfrac {2a-{b}^{2}}{1}=1\times 6=6\\ -\dfrac {-2-a}{1}=1+6=7\end{matrix} \right.$
得$x=5$ $b=\pm 2$.