题目
点(1,1,0)到直线(1,1,0)的距离为___________.
点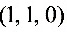
到直线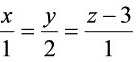
的距离为___________.
题目解答
答案
[答案]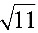
[详解] 令 A=(1,1,0), B=(0,0,3),则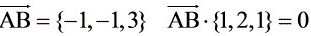
所以,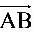
垂直该直线,点A(1,1,0)到该直线的最短距离为
=.
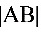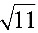解析
步骤 1：确定直线的方向向量
直线$\dfrac {x}{1}=\dfrac {y}{2}=\dfrac {z-3}{1}$的方向向量为$\vec{d}=\{1,2,1\}$。
步骤 2：确定点A到直线上一点B的向量
点A(1,1,0)到直线上一点B(0,0,3)的向量为$\overrightarrow {AB}=\{ -1,-1,3\} $。
步骤 3：计算$\overrightarrow {AB}$与直线方向向量$\vec{d}$的点积
$\overrightarrow {AB}\cdot \vec{d}=\{ -1,-1,3\} \cdot \{1,2,1\} = -1*1 + (-1)*2 + 3*1 = -1 - 2 + 3 = 0$，说明$\overrightarrow {AB}$垂直于直线方向向量$\vec{d}$。
步骤 4：计算点A到直线的距离
点A到直线的距离即为向量$\overrightarrow {AB}$的模长，即$|\overrightarrow {AB}|=\sqrt{(-1)^2+(-1)^2+3^2}=\sqrt{1+1+9}=\sqrt{11}$。
直线$\dfrac {x}{1}=\dfrac {y}{2}=\dfrac {z-3}{1}$的方向向量为$\vec{d}=\{1,2,1\}$。
步骤 2：确定点A到直线上一点B的向量
点A(1,1,0)到直线上一点B(0,0,3)的向量为$\overrightarrow {AB}=\{ -1,-1,3\} $。
步骤 3：计算$\overrightarrow {AB}$与直线方向向量$\vec{d}$的点积
$\overrightarrow {AB}\cdot \vec{d}=\{ -1,-1,3\} \cdot \{1,2,1\} = -1*1 + (-1)*2 + 3*1 = -1 - 2 + 3 = 0$，说明$\overrightarrow {AB}$垂直于直线方向向量$\vec{d}$。
步骤 4：计算点A到直线的距离
点A到直线的距离即为向量$\overrightarrow {AB}$的模长，即$|\overrightarrow {AB}|=\sqrt{(-1)^2+(-1)^2+3^2}=\sqrt{1+1+9}=\sqrt{11}$。