题目
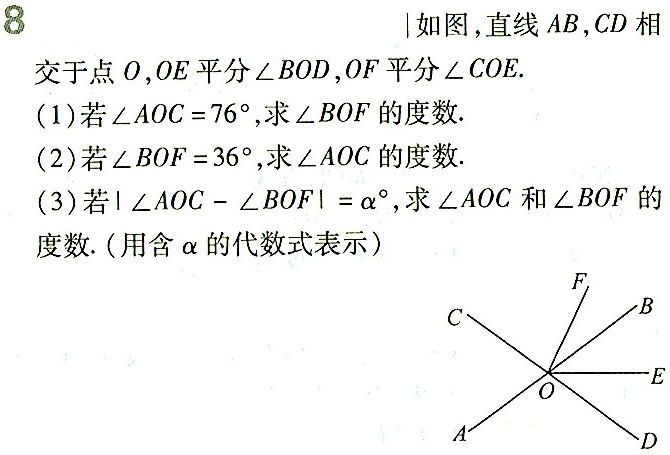
|如图,直线AB,CD相.-|||-交于点O,OE平分 angle BOD, OF平分 angle COE.-|||-(1)若 angle AOC=(76)^circ , 求 angle BOF 的度数.-|||-(2)若 angle BOF=(36)^circ , 求 angle AOC 的度数.-|||-(3)若| angle AOC-angle BOF|=(alpha )^circ , 求 angle AOC 和 angle BOF 的-|||-度数.(用含α的代数式表示)-|||-F,-|||-C B-|||-0-|||-E-|||-A D
题目解答
答案

解析
步骤 1:确定 $\angle BOD$ 的度数
由于 $\angle AOC$ 和 $\angle BOD$ 是对顶角,它们的度数相等。因此,$\angle BOD = \angle AOC = 76^\circ$。
步骤 2:确定 $\angle BOE$ 和 $\angle DOE$ 的度数
因为OE平分 $\angle BOD$,所以 $\angle BOE = \angle DOE = \frac{1}{2} \angle BOD = \frac{1}{2} \times 76^\circ = 38^\circ$。
步骤 3:确定 $\angle COE$ 的度数
$\angle COE$ 是 $\angle BOD$ 的补角,所以 $\angle COE = 180^\circ - \angle BOD = 180^\circ - 76^\circ = 104^\circ$。
步骤 4:确定 $\angle EOF$ 的度数
因为OF平分 $\angle COE$,所以 $\angle EOF = \frac{1}{2} \angle COE = \frac{1}{2} \times 104^\circ = 52^\circ$。
步骤 5:确定 $\angle BOF$ 的度数
$\angle BOF = \angle EOF - \angle BOE = 52^\circ - 38^\circ = 14^\circ$。
步骤 6:确定 $\angle AOC$ 的度数
因为 $\angle BOF = 36^\circ$,我们设 $\angle BOE = x$,则 $\angle DOE = x$,$\angle COA = \angle BOD = 2x$,$\angle EOF = \angle COF = x + 36^\circ$。根据 $\angle AOC + \angle COF + \angle BOF = 180^\circ$,我们有 $2x + x + 36^\circ + 36^\circ = 180^\circ$,解得 $x = 36^\circ$,所以 $\angle AOC = 2x = 72^\circ$。
步骤 7:确定 $\angle AOC$ 和 $\angle BOF$ 的度数
设 $\angle BOE = x$,则 $\angle DOE = x$,$\angle COA = \angle BOD = 2x$,$\angle BOC = 180^\circ - 2x$,$\angle COF = \angle EOF = x + \angle BOF$。根据 $\angle BOF = 90^\circ - \frac{3}{2}x$,我们有 $|2x - (90^\circ - \frac{3}{2}x)| = \alpha^\circ$,解得 $x = \frac{180}{7} + \frac{2}{7}\alpha$ 或 $x = \frac{180}{7} - \frac{2}{7}\alpha$。因此,$\angle AOC = 2x = \frac{360}{7} + \frac{4}{7}\alpha$ 或 $\angle AOC = \frac{360}{7} - \frac{4}{7}\alpha$,$\angle BOF = 90^\circ - \frac{3}{2}x = \frac{360}{7} - \frac{3}{7}\alpha$ 或 $\angle BOF = \frac{360}{7} + \frac{3}{7}\alpha$。
由于 $\angle AOC$ 和 $\angle BOD$ 是对顶角,它们的度数相等。因此,$\angle BOD = \angle AOC = 76^\circ$。
步骤 2:确定 $\angle BOE$ 和 $\angle DOE$ 的度数
因为OE平分 $\angle BOD$,所以 $\angle BOE = \angle DOE = \frac{1}{2} \angle BOD = \frac{1}{2} \times 76^\circ = 38^\circ$。
步骤 3:确定 $\angle COE$ 的度数
$\angle COE$ 是 $\angle BOD$ 的补角,所以 $\angle COE = 180^\circ - \angle BOD = 180^\circ - 76^\circ = 104^\circ$。
步骤 4:确定 $\angle EOF$ 的度数
因为OF平分 $\angle COE$,所以 $\angle EOF = \frac{1}{2} \angle COE = \frac{1}{2} \times 104^\circ = 52^\circ$。
步骤 5:确定 $\angle BOF$ 的度数
$\angle BOF = \angle EOF - \angle BOE = 52^\circ - 38^\circ = 14^\circ$。
步骤 6:确定 $\angle AOC$ 的度数
因为 $\angle BOF = 36^\circ$,我们设 $\angle BOE = x$,则 $\angle DOE = x$,$\angle COA = \angle BOD = 2x$,$\angle EOF = \angle COF = x + 36^\circ$。根据 $\angle AOC + \angle COF + \angle BOF = 180^\circ$,我们有 $2x + x + 36^\circ + 36^\circ = 180^\circ$,解得 $x = 36^\circ$,所以 $\angle AOC = 2x = 72^\circ$。
步骤 7:确定 $\angle AOC$ 和 $\angle BOF$ 的度数
设 $\angle BOE = x$,则 $\angle DOE = x$,$\angle COA = \angle BOD = 2x$,$\angle BOC = 180^\circ - 2x$,$\angle COF = \angle EOF = x + \angle BOF$。根据 $\angle BOF = 90^\circ - \frac{3}{2}x$,我们有 $|2x - (90^\circ - \frac{3}{2}x)| = \alpha^\circ$,解得 $x = \frac{180}{7} + \frac{2}{7}\alpha$ 或 $x = \frac{180}{7} - \frac{2}{7}\alpha$。因此,$\angle AOC = 2x = \frac{360}{7} + \frac{4}{7}\alpha$ 或 $\angle AOC = \frac{360}{7} - \frac{4}{7}\alpha$,$\angle BOF = 90^\circ - \frac{3}{2}x = \frac{360}{7} - \frac{3}{7}\alpha$ 或 $\angle BOF = \frac{360}{7} + \frac{3}{7}\alpha$。