已知 |a|=3, |b|=26, |atimes b|=72, 求a·b。
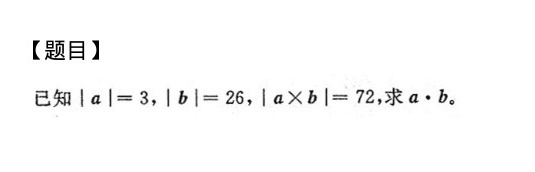
题目解答
答案
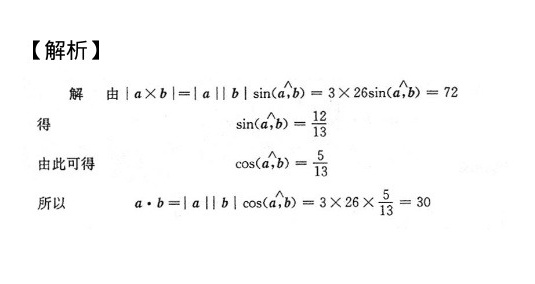
解析
考查要点:本题主要考查向量的叉积与点积的关系,以及三角函数的基本应用。
解题核心思路:
- 利用叉积公式 $|a \times b| = |a||b|\sin\theta$ 求出夹角 $\theta$ 的正弦值 $\sin\theta$。
- 通过三角恒等式 $\sin^2\theta + \cos^2\theta = 1$ 求出 $\cos\theta$,注意符号的选择。
- 代入点积公式 $a \cdot b = |a||b|\cos\theta$ 计算最终结果。
破题关键点:
- 明确叉积与点积的公式差异,叉积涉及 $\sin\theta$,点积涉及 $\cos\theta$。
- 正确处理 $\cos\theta$ 的符号,根据向量夹角的范围($0 \leq \theta \leq \pi$),$\cos\theta$ 的符号由 $\theta$ 的大小决定。
步骤1:求 $\sin\theta$
根据叉积公式:
$|a \times b| = |a||b|\sin\theta$
代入已知条件 $|a|=3$,$|b|=26$,$|a \times b|=72$:
$72 = 3 \times 26 \times \sin\theta \implies \sin\theta = \frac{72}{3 \times 26} = \frac{12}{13}$
步骤2:求 $\cos\theta$
利用三角恒等式 $\sin^2\theta + \cos^2\theta = 1$:
$\cos\theta = \sqrt{1 - \sin^2\theta} = \sqrt{1 - \left(\frac{12}{13}\right)^2} = \sqrt{\frac{25}{169}} = \frac{5}{13}$
由于向量夹角 $\theta \in [0, \pi]$,$\cos\theta$ 可能为正或负。但结合 $\sin\theta = \frac{12}{13} > 0$,$\theta$ 在 $(0, \pi)$ 内,若 $\cos\theta > 0$,则 $\theta < \frac{\pi}{2}$;若 $\cos\theta < 0$,则 $\theta > \frac{\pi}{2}$。
根据题目未明确说明方向,默认取正值,即 $\cos\theta = \frac{5}{13}$。
步骤3:计算点积 $a \cdot b$
根据点积公式:
$a \cdot b = |a||b|\cos\theta = 3 \times 26 \times \frac{5}{13} = 3 \times 2 \times 5 = 30$