题目
lim _(xarrow infty )((1-dfrac {1)(2x))}^x+2= ).A.lim _(xarrow infty )((1-dfrac {1)(2x))}^x+2= )B.lim _(xarrow infty )((1-dfrac {1)(2x))}^x+2= )C.lim _(xarrow infty )((1-dfrac {1)(2x))}^x+2= )D.lim _(xarrow infty )((1-dfrac {1)(2x))}^x+2= )
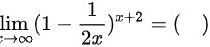 .
.
A.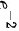
B.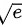
C.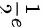
D.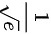
题目解答
答案
利用重要极限公式求解,则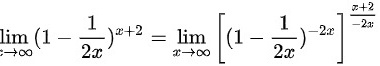
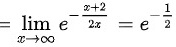 ,因此选择D.
,因此选择D.
解析
考查要点:本题主要考查利用重要极限公式求解极限的能力,需要灵活处理底数和指数的变形。
解题核心思路:
将题目中的表达式转化为重要极限形式$\lim_{x \to \infty} \left(1 + \frac{a}{x}\right)^x = e^a$,通过调整底数和指数的结构,结合指数运算的性质求解。
破题关键点:
- 底数变形:将$1 - \frac{1}{2x}$改写为$\left(1 + \frac{-1}{2x}\right)$,对应重要极限中的$a = -\frac{1}{2}$。
- 指数拆分:将原指数$x+2$拆分为与底数变形后的指数相关联的形式,利用$\lim_{x \to \infty} \frac{x+2}{2x} = \frac{1}{2}$简化计算。
步骤1:调整底数形式
将原式改写为:
$\lim_{x \to \infty} \left(1 - \frac{1}{2x}\right)^{x+2} = \lim_{x \to \infty} \left[\left(1 - \frac{1}{2x}\right)^{-2x}\right]^{\frac{x+2}{-2x}}.$
步骤2:应用重要极限公式
根据重要极限$\lim_{x \to \infty} \left(1 + \frac{a}{x}\right)^x = e^a$,当$a = -\frac{1}{2}$时,有:
$\lim_{x \to \infty} \left(1 - \frac{1}{2x}\right)^{-2x} = e^{-1}.$
步骤3:处理外部指数
外部指数$\frac{x+2}{-2x}$的极限为:
$\lim_{x \to \infty} \frac{x+2}{-2x} = -\frac{1}{2}.$
步骤4:综合结果
将两部分结合,得到:
$\left(e^{-1}\right)^{-\frac{1}{2}} = e^{\frac{1}{2}} = \frac{1}{\sqrt{e}}.$