题目
求解微分方程 '+y-x(e)^-(x^2)=0 的通解..
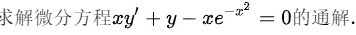 .
.
题目解答
答案
解:

解析
考查要点:本题主要考查一阶线性微分方程的解法,需要掌握积分因子法的应用。
解题核心思路:
- 将原方程整理为标准形式$y' + P(x)y = Q(x)$,确定$P(x)$和$Q(x)$。
- 计算积分因子$\mu(x) = e^{\int P(x) dx}$,并对方程两边同乘积分因子,将方程转化为全微分形式。
- 对全微分方程两边积分,得到通解。
破题关键点:
- 识别方程类型:通过整理方程结构,确认为一阶线性微分方程。
- 正确计算积分因子:注意积分因子的计算需对$P(x)$积分。
- 处理特殊积分:右侧积分$\int x e^{-x^2} dx$需用换元法。
将原方程$xy' + y = x e^{-x^2}$整理为标准形式:
$y' + \frac{1}{x} y = e^{-x^2}$
步骤1:计算积分因子
积分因子为:
$\mu(x) = e^{\int \frac{1}{x} dx} = e^{\ln |x|} = x$
步骤2:方程两边同乘积分因子
原方程变为:
$x y' + y = x e^{-x^2}$
左边可写为全微分形式:
$\frac{d}{dx}(x y) = x e^{-x^2}$
步骤3:积分求解
对两边积分:
$\int \frac{d}{dx}(x y) dx = \int x e^{-x^2} dx$
左边积分结果为$x y$,右边通过换元法计算:
令$u = -x^2$,则$du = -2x dx$,即$x dx = -\frac{1}{2} du$,得:
$\int x e^{-x^2} dx = -\frac{1}{2} \int e^u du = -\frac{1}{2} e^u + C = -\frac{1}{2} e^{-x^2} + C$
步骤4:整理通解
联立得:
$x y = -\frac{1}{2} e^{-x^2} + C$
解得通解:
$y = -\frac{1}{2x} e^{-x^2} + \frac{C}{x}$