题目
设二元函数z=f(x,y)的全微分z=f(x,y), 则z=f(x,y)
设二元函数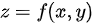 的全微分
的全微分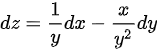 , 则
, 则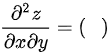
题目解答
答案
答案:选
由题意,已知
二元函数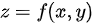 的全微分
的全微分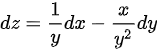
根据二元函数的全微分公式,知
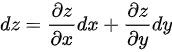
∴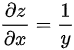
将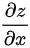 对
对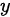 求导,得
求导,得
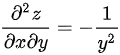
解析
步骤 1:确定全微分的表达式
已知二元函数z=f(x,y)的全微分$dz=\dfrac {1}{y}dx-\dfrac {x}{{y}^{2}}dy$,根据全微分的定义,有$dz=\dfrac {\partial z}{\partial x}dx+\dfrac {\partial z}{\partial y}dy$。
步骤 2:确定偏导数
比较全微分的表达式,可以得到$\dfrac {\partial z}{\partial x}=\dfrac {1}{y}$和$\dfrac {\partial z}{\partial y}=-\dfrac {x}{{y}^{2}}$。
步骤 3:计算混合偏导数
为了求$\dfrac {{\partial }^{2}z}{\partial x\partial y}$,需要对$\dfrac {\partial z}{\partial x}$关于y求偏导数,即$\dfrac {\partial }{\partial y}(\dfrac {\partial z}{\partial x})$。根据步骤2中的$\dfrac {\partial z}{\partial x}=\dfrac {1}{y}$,对y求偏导数,得到$\dfrac {{\partial }^{2}z}{\partial x\partial y}=-\dfrac {1}{{y}^{2}}$。
已知二元函数z=f(x,y)的全微分$dz=\dfrac {1}{y}dx-\dfrac {x}{{y}^{2}}dy$,根据全微分的定义,有$dz=\dfrac {\partial z}{\partial x}dx+\dfrac {\partial z}{\partial y}dy$。
步骤 2:确定偏导数
比较全微分的表达式,可以得到$\dfrac {\partial z}{\partial x}=\dfrac {1}{y}$和$\dfrac {\partial z}{\partial y}=-\dfrac {x}{{y}^{2}}$。
步骤 3:计算混合偏导数
为了求$\dfrac {{\partial }^{2}z}{\partial x\partial y}$,需要对$\dfrac {\partial z}{\partial x}$关于y求偏导数,即$\dfrac {\partial }{\partial y}(\dfrac {\partial z}{\partial x})$。根据步骤2中的$\dfrac {\partial z}{\partial x}=\dfrac {1}{y}$,对y求偏导数,得到$\dfrac {{\partial }^{2}z}{\partial x\partial y}=-\dfrac {1}{{y}^{2}}$。