题目
求函数 (x)=dfrac ({x)^3+3(x)^2-x-3}({x)^2+x-6} 的连续区间,并 求 极限 lim f(x),-|||-limf(x)及lim f(x).
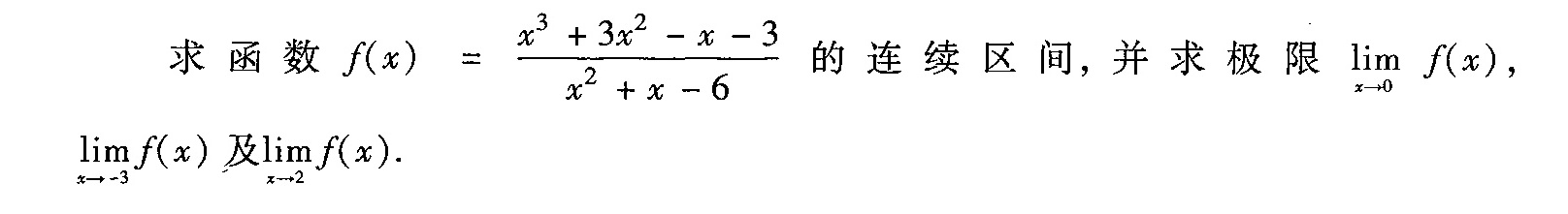
题目解答
答案

解析
考查要点:本题主要考查分式函数的连续区间判断及极限的计算,涉及分式函数的定义域、因式分解、极限存在性判断及计算方法。
解题核心思路:
- 确定连续区间:分式函数连续的条件是分母不为零,因此需先求出分母为零的点,排除这些点后得到连续区间。
- 计算极限:
- 直接代入法:当趋近点在定义域内时,直接代入计算。
- 化简约分法:当趋近点使分母为零但分子不为零时,极限不存在(趋向无穷);若分子分母均为零,则通过因式分解约分后计算。
破题关键点:
- 分母因式分解:找到分母的零点,确定间断点。
- 分子因式分解:判断趋近点是否为可去间断点或无穷间断点。
- 极限方向分析:趋近于分母为零的点时,需分析左右极限的符号。
1. 确定连续区间
分母为 $x^2 + x - 6$,因式分解得:
$x^2 + x - 6 = (x + 3)(x - 2)$
因此,分母在 $x = -3$ 和 $x = 2$ 时为零,函数在这些点无定义。
连续区间为:$(-\infty, -3)$,$(-3, 2)$,$(2, +\infty)$。
2. 计算极限
$\lim\limits_{x \to 0} f(x)$
直接代入 $x = 0$:
$f(0) = \frac{0^3 + 3 \cdot 0^2 - 0 - 3}{0^2 + 0 - 6} = \frac{-3}{-6} = \frac{1}{2}$
$\lim\limits_{x \to -3} f(x)$
- 检查分子是否为零:代入 $x = -3$:
$(-3)^3 + 3(-3)^2 - (-3) - 3 = -27 + 27 + 3 - 3 = 0$
分子也为零,说明可约分。 - 因式分解:
- 分子:$x^3 + 3x^2 - x - 3 = (x + 3)(x^2 - 1)$
- 分母:$(x + 3)(x - 2)$
约分后得:
$f(x) = \frac{x^2 - 1}{x - 2} \quad (x \neq -3)$
- 代入化简后的表达式:
$\lim_{x \to -3} \frac{x^2 - 1}{x - 2} = \frac{(-3)^2 - 1}{-3 - 2} = \frac{8}{-5} = -\frac{8}{5}$
$\lim\limits_{x \to 2} f(x)$
- 检查分子是否为零:代入 $x = 2$:
$2^3 + 3 \cdot 2^2 - 2 - 3 = 8 + 12 - 2 - 3 = 15 \neq 0$
分母为零,分子非零,极限趋向无穷。 - 分析方向:
- 当 $x \to 2^+$ 时,分母 $(x - 2) \to 0^+$,分子为正,极限为 $+\infty$。
- 当 $x \to 2^-$ 时,分母 $(x - 2) \to 0^-$,分子为正,极限为 $-\infty$。
因此,$\lim\limits_{x \to 2} f(x)$ 不存在,趋向无穷大。