题目
已知曲线 =asqrt (x)(agt 0) 与曲线 =ln sqrt (x) 在点(x0,y0)处有公共切已知曲线 =asqrt (x)(agt 0) 与曲线 =ln sqrt (x) 在点(x0,y0)处有公共切

题目解答
答案
解析:
解析
步骤 1:求导数
对曲线 $y=a\sqrt{x}$ 求导,得到 $y'=\frac{a}{2\sqrt{x}}$。对曲线 $y=\ln\sqrt{x}$ 求导,得到 $y'=\frac{1}{2x}$。
步骤 2:求切点
由于两曲线在点 $(x_0,y_0)$ 处有公共切线,因此它们的导数相等,即 $\frac{a}{2\sqrt{x_0}}=\frac{1}{2x_0}$。解得 $x_0=\frac{1}{a^2}$。
步骤 3:求常数a及切点
将 $x_0=\frac{1}{a^2}$ 分别代入两曲线方程,得到 $y_0=a\sqrt{\frac{1}{a^2}}=\frac{1}{2}\ln\frac{1}{a^2}$。解得 $a=\frac{1}{e}$,$x_0=e^2$,$y_0=1$。因此,切点为 $(e^2,1)$。
步骤 4:求面积S
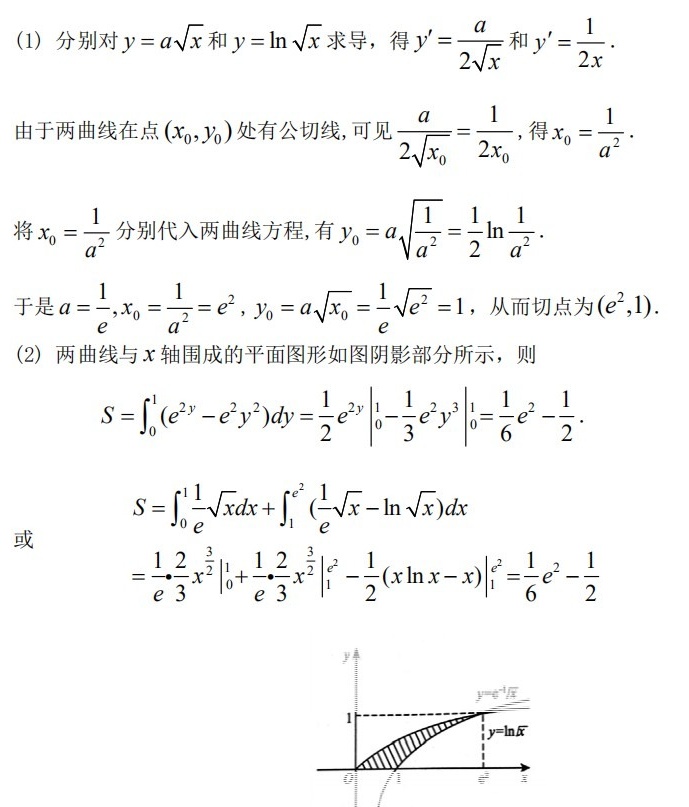
两曲线与x轴围成的平面图形如图阴影部分所示,因此 $S=\int_{0}^{1}(\frac{1}{e}\sqrt{x}-\ln\sqrt{x})dx$。计算得 $S=\frac{1}{6}e^2-\frac{1}{2}$。
对曲线 $y=a\sqrt{x}$ 求导,得到 $y'=\frac{a}{2\sqrt{x}}$。对曲线 $y=\ln\sqrt{x}$ 求导,得到 $y'=\frac{1}{2x}$。
步骤 2:求切点
由于两曲线在点 $(x_0,y_0)$ 处有公共切线,因此它们的导数相等,即 $\frac{a}{2\sqrt{x_0}}=\frac{1}{2x_0}$。解得 $x_0=\frac{1}{a^2}$。
步骤 3:求常数a及切点
将 $x_0=\frac{1}{a^2}$ 分别代入两曲线方程,得到 $y_0=a\sqrt{\frac{1}{a^2}}=\frac{1}{2}\ln\frac{1}{a^2}$。解得 $a=\frac{1}{e}$,$x_0=e^2$,$y_0=1$。因此,切点为 $(e^2,1)$。
步骤 4:求面积S
两曲线与x轴围成的平面图形如图阴影部分所示,因此 $S=\int_{0}^{1}(\frac{1}{e}\sqrt{x}-\ln\sqrt{x})dx$。计算得 $S=\frac{1}{6}e^2-\frac{1}{2}$。