题目
30 A-|||-C-|||-M N如图所示，某居民小区的A，B两楼之间的距离MN=30m，两楼高都是20m，A楼在B楼正南，B楼一楼朝南的窗台离地面的距离CN=2m，窗户高1.8m，正午时刻太阳光线与地面成30°角，A楼的影子是否影响B楼一楼窗户采光？若影响，挡住窗户多高？若不影响，请说明理由．（参考数据：sqrt(2)≈1.414，sqrt(3)≈1.732，sqrt(5)≈2.236）
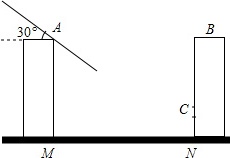如图所示，某居民小区的A，B两楼之间的距离MN=30m，两楼高都是20m，A楼在B楼正南，B楼一楼朝南的窗台离地面的距离CN=2m，窗户高1.8m，正午时刻太阳光线与地面成30°角，A楼的影子是否影响B楼一楼窗户采光？若影响，挡住窗户多高？若不影响，请说明理由．（参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732，$\sqrt{5}$≈2.236）题目解答
答案
解：有影响．
设过E点的光线交地面于G点，如图，EM=FN=20m，MN=30m，CN=2m，CD=1.8m，
在Rt△EMG中，∵∠EGM=30°，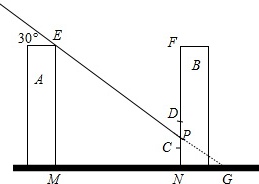
∴MG=$\sqrt{3}$EM=20$\sqrt{3}$≈34.64＞30，
∴A楼的影子要落在B楼上，
设PN为A楼在B楼上的影长，
在Rt△PNG中，∵∠PGN=30°，NG=MG-MN=20$\sqrt{3}$-30，
∴PN=$\frac{\sqrt{3}}{3}$NG=20-10$\sqrt{3}$≈2.68，
∴PN-CN=2.68-2=0.68（m）．
答：A楼影子影响到B楼一楼采光，挡住该户窗户0.68米．
设过E点的光线交地面于G点，如图，EM=FN=20m，MN=30m，CN=2m，CD=1.8m，
在Rt△EMG中，∵∠EGM=30°，
∴MG=$\sqrt{3}$EM=20$\sqrt{3}$≈34.64＞30，
∴A楼的影子要落在B楼上，
设PN为A楼在B楼上的影长，
在Rt△PNG中，∵∠PGN=30°，NG=MG-MN=20$\sqrt{3}$-30，
∴PN=$\frac{\sqrt{3}}{3}$NG=20-10$\sqrt{3}$≈2.68，
∴PN-CN=2.68-2=0.68（m）．
答：A楼影子影响到B楼一楼采光，挡住该户窗户0.68米．
解析
步骤 1：确定A楼影子的长度
在正午时刻，太阳光线与地面成30°角，A楼高20m，因此A楼的影子长度可以通过直角三角形的性质计算。设A楼的影子长度为x，则有：
$$
\tan(30°) = \frac{20}{x}
$$
解得：
$$
x = \frac{20}{\tan(30°)} = \frac{20}{\frac{\sqrt{3}}{3}} = 20\sqrt{3} \approx 34.64m
$$
步骤 2：判断A楼影子是否影响B楼一楼窗户采光
A楼与B楼之间的距离为30m，而A楼的影子长度为34.64m，因此A楼的影子会落在B楼上，影响B楼一楼窗户采光。
步骤 3：计算A楼影子挡住B楼窗户的高度
设A楼影子在B楼上的投影长度为y，则有：
$$
y = x - MN = 34.64 - 30 = 4.64m
$$
在B楼一楼窗户处，A楼影子的高度为：
$$
h = y \cdot \tan(30°) = 4.64 \cdot \frac{\sqrt{3}}{3} = 4.64 \cdot \frac{1.732}{3} \approx 2.68m
$$
因此，A楼影子挡住B楼窗户的高度为：
$$
h - CN = 2.68 - 2 = 0.68m
$$
在正午时刻，太阳光线与地面成30°角，A楼高20m，因此A楼的影子长度可以通过直角三角形的性质计算。设A楼的影子长度为x，则有：
$$
\tan(30°) = \frac{20}{x}
$$
解得：
$$
x = \frac{20}{\tan(30°)} = \frac{20}{\frac{\sqrt{3}}{3}} = 20\sqrt{3} \approx 34.64m
$$
步骤 2：判断A楼影子是否影响B楼一楼窗户采光
A楼与B楼之间的距离为30m，而A楼的影子长度为34.64m，因此A楼的影子会落在B楼上，影响B楼一楼窗户采光。
步骤 3：计算A楼影子挡住B楼窗户的高度
设A楼影子在B楼上的投影长度为y，则有：
$$
y = x - MN = 34.64 - 30 = 4.64m
$$
在B楼一楼窗户处，A楼影子的高度为：
$$
h = y \cdot \tan(30°) = 4.64 \cdot \frac{\sqrt{3}}{3} = 4.64 \cdot \frac{1.732}{3} \approx 2.68m
$$
因此，A楼影子挡住B楼窗户的高度为：
$$
h - CN = 2.68 - 2 = 0.68m
$$