题目
13.设方程 ln (y-x)+cos (xy)-1=y 确定函数 y=y(x) ,则 ''(0)= __

题目解答
答案
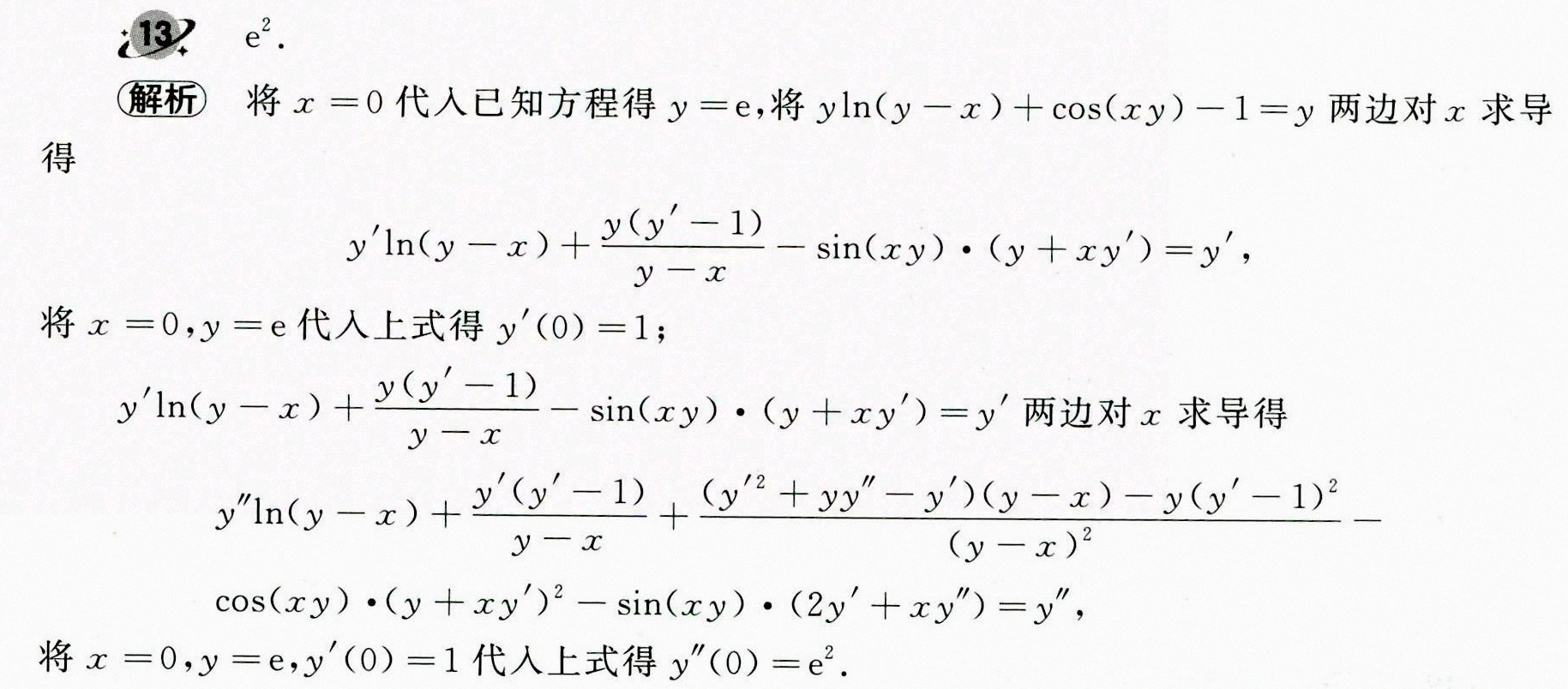
解析
步骤 1:代入初始条件
将 $x=0$ 代入方程 $y\ln (y-x)+\cos (xy)-1=y$,得到 $y\ln y+\cos 0-1=y$,即 $y\ln y=y$。解得 $y=e$。
步骤 2:对原方程求导
对原方程 $y\ln (y-x)+\cos (xy)-1=y$ 两边对 $x$ 求导,得到:
$$
y'\ln (y-x)+\frac{y}{y-x}y'-y\sin (xy)y'-y'=0
$$
步骤 3:代入 $x=0$ 和 $y=e$
将 $x=0$ 和 $y=e$ 代入上式,得到:
$$
y'\ln e+\frac{e}{e}y'-e\sin 0y'-y'=0
$$
化简得:
$$
y'+y'-y'=0
$$
解得 $y'(0)=1$。
步骤 4:对导数方程求导
对导数方程 $y'\ln (y-x)+\frac{y}{y-x}y'-y\sin (xy)y'-y'=0$ 两边对 $x$ 求导,得到:
$$
y''\ln (y-x)+\frac{y'}{y-x}y'-\frac{y(y')^2}{(y-x)^2}+y'\frac{y}{y-x}-y\sin (xy)y''-y\cos (xy)(y')^2-y''=0
$$
步骤 5:代入 $x=0$,$y=e$ 和 $y'(0)=1$
将 $x=0$,$y=e$ 和 $y'(0)=1$ 代入上式,得到:
$$
y''\ln e+\frac{1}{e}y'-\frac{e}{e^2}+y'\frac{e}{e}-e\sin 0y''-e\cos 0(1)^2-y''=0
$$
化简得:
$$
y''+y''-y''=e^2
$$
解得 $y''(0)=e^2$。
将 $x=0$ 代入方程 $y\ln (y-x)+\cos (xy)-1=y$,得到 $y\ln y+\cos 0-1=y$,即 $y\ln y=y$。解得 $y=e$。
步骤 2:对原方程求导
对原方程 $y\ln (y-x)+\cos (xy)-1=y$ 两边对 $x$ 求导,得到:
$$
y'\ln (y-x)+\frac{y}{y-x}y'-y\sin (xy)y'-y'=0
$$
步骤 3:代入 $x=0$ 和 $y=e$
将 $x=0$ 和 $y=e$ 代入上式,得到:
$$
y'\ln e+\frac{e}{e}y'-e\sin 0y'-y'=0
$$
化简得:
$$
y'+y'-y'=0
$$
解得 $y'(0)=1$。
步骤 4:对导数方程求导
对导数方程 $y'\ln (y-x)+\frac{y}{y-x}y'-y\sin (xy)y'-y'=0$ 两边对 $x$ 求导,得到:
$$
y''\ln (y-x)+\frac{y'}{y-x}y'-\frac{y(y')^2}{(y-x)^2}+y'\frac{y}{y-x}-y\sin (xy)y''-y\cos (xy)(y')^2-y''=0
$$
步骤 5:代入 $x=0$,$y=e$ 和 $y'(0)=1$
将 $x=0$,$y=e$ 和 $y'(0)=1$ 代入上式,得到:
$$
y''\ln e+\frac{1}{e}y'-\frac{e}{e^2}+y'\frac{e}{e}-e\sin 0y''-e\cos 0(1)^2-y''=0
$$
化简得:
$$
y''+y''-y''=e^2
$$
解得 $y''(0)=e^2$。