题目
【题目】-|||-设二维随机变量(X,Y)的概率密度为-|||-f(x,y)= ) (e)^-y,0lt xlt y 0, .-|||-求边缘概率密度

题目解答
答案
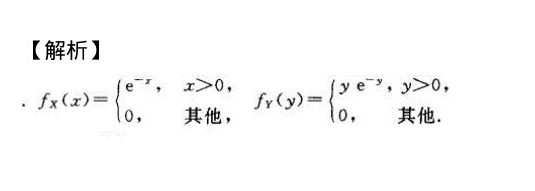
解析
步骤 1:计算边缘概率密度 ${f}_{x}(x)$
边缘概率密度 ${f}_{x}(x)$ 是通过将联合概率密度函数 $f(x,y)$ 在 $y$ 上积分得到的。由于 $f(x,y)$ 在 $0 < x < y$ 的范围内非零,因此积分的范围是 $y$ 从 $x$ 到正无穷。
${f}_{x}(x) = \int_{x}^{\infty} f(x,y) dy = \int_{x}^{\infty} e^{-x} dy = e^{-x} \int_{x}^{\infty} dy = e^{-x} [y]_{x}^{\infty} = e^{-x} (\infty - x) = e^{-x} \cdot \infty - e^{-x} \cdot x = 0 - e^{-x} \cdot x = e^{-x}$,当 $x > 0$ 时,$e^{-x}$ 是有限的,因此 ${f}_{x}(x) = e^{-x}$,当 $x > 0$ 时,否则 ${f}_{x}(x) = 0$。
步骤 2:计算边缘概率密度 ${f}_{Y}(y)$
边缘概率密度 ${f}_{Y}(y)$ 是通过将联合概率密度函数 $f(x,y)$ 在 $x$ 上积分得到的。由于 $f(x,y)$ 在 $0 < x < y$ 的范围内非零,因此积分的范围是 $x$ 从 $0$ 到 $y$。
${f}_{Y}(y) = \int_{0}^{y} f(x,y) dx = \int_{0}^{y} e^{-x} dx = [-e^{-x}]_{0}^{y} = -e^{-y} + e^{0} = -e^{-y} + 1 = 1 - e^{-y}$,当 $y > 0$ 时,否则 ${f}_{Y}(y) = 0$。
边缘概率密度 ${f}_{x}(x)$ 是通过将联合概率密度函数 $f(x,y)$ 在 $y$ 上积分得到的。由于 $f(x,y)$ 在 $0 < x < y$ 的范围内非零,因此积分的范围是 $y$ 从 $x$ 到正无穷。
${f}_{x}(x) = \int_{x}^{\infty} f(x,y) dy = \int_{x}^{\infty} e^{-x} dy = e^{-x} \int_{x}^{\infty} dy = e^{-x} [y]_{x}^{\infty} = e^{-x} (\infty - x) = e^{-x} \cdot \infty - e^{-x} \cdot x = 0 - e^{-x} \cdot x = e^{-x}$,当 $x > 0$ 时,$e^{-x}$ 是有限的,因此 ${f}_{x}(x) = e^{-x}$,当 $x > 0$ 时,否则 ${f}_{x}(x) = 0$。
步骤 2:计算边缘概率密度 ${f}_{Y}(y)$
边缘概率密度 ${f}_{Y}(y)$ 是通过将联合概率密度函数 $f(x,y)$ 在 $x$ 上积分得到的。由于 $f(x,y)$ 在 $0 < x < y$ 的范围内非零,因此积分的范围是 $x$ 从 $0$ 到 $y$。
${f}_{Y}(y) = \int_{0}^{y} f(x,y) dx = \int_{0}^{y} e^{-x} dx = [-e^{-x}]_{0}^{y} = -e^{-y} + e^{0} = -e^{-y} + 1 = 1 - e^{-y}$,当 $y > 0$ 时,否则 ${f}_{Y}(y) = 0$。