题目
求不定积分int dfrac (1)(xsqrt {{x)^2-1}}dx。
求不定积分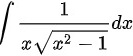 。
。
题目解答
答案
令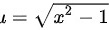 ,那么
,那么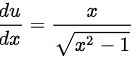 ,
,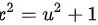 使得
使得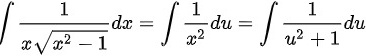
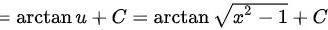 。
。
综上,本题答案为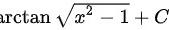
解析
步骤 1:代换
令 $u = \sqrt{x^2 - 1}$,则 $u^2 = x^2 - 1$,从而 $x^2 = u^2 + 1$。对 $u$ 关于 $x$ 求导,得到 $\dfrac{du}{dx} = \dfrac{x}{\sqrt{x^2 - 1}}$,即 $dx = \dfrac{\sqrt{x^2 - 1}}{x}du$。
步骤 2:代入
将 $u$ 和 $dx$ 的表达式代入原积分,得到 $\int \dfrac{1}{x\sqrt{x^2 - 1}}dx = \int \dfrac{1}{x\sqrt{x^2 - 1}} \cdot \dfrac{\sqrt{x^2 - 1}}{x}du = \int \dfrac{1}{x^2}du$。
步骤 3:简化
由于 $x^2 = u^2 + 1$,则 $\int \dfrac{1}{x^2}du = \int \dfrac{1}{u^2 + 1}du$。
步骤 4:积分
$\int \dfrac{1}{u^2 + 1}du = \arctan u + C$。
步骤 5:回代
将 $u = \sqrt{x^2 - 1}$ 回代,得到 $\arctan \sqrt{x^2 - 1} + C$。
令 $u = \sqrt{x^2 - 1}$,则 $u^2 = x^2 - 1$,从而 $x^2 = u^2 + 1$。对 $u$ 关于 $x$ 求导,得到 $\dfrac{du}{dx} = \dfrac{x}{\sqrt{x^2 - 1}}$,即 $dx = \dfrac{\sqrt{x^2 - 1}}{x}du$。
步骤 2:代入
将 $u$ 和 $dx$ 的表达式代入原积分,得到 $\int \dfrac{1}{x\sqrt{x^2 - 1}}dx = \int \dfrac{1}{x\sqrt{x^2 - 1}} \cdot \dfrac{\sqrt{x^2 - 1}}{x}du = \int \dfrac{1}{x^2}du$。
步骤 3:简化
由于 $x^2 = u^2 + 1$,则 $\int \dfrac{1}{x^2}du = \int \dfrac{1}{u^2 + 1}du$。
步骤 4:积分
$\int \dfrac{1}{u^2 + 1}du = \arctan u + C$。
步骤 5:回代
将 $u = \sqrt{x^2 - 1}$ 回代,得到 $\arctan \sqrt{x^2 - 1} + C$。