题目
设n是非齐次线性方程组 Ax=b 的一个特解, ξ1,ξ2,···· _(n-1) 是其导出-|||-方程组的一个基础解系,则ξ1,52,··· _(n-1) n线性无关.A.正确B.错误
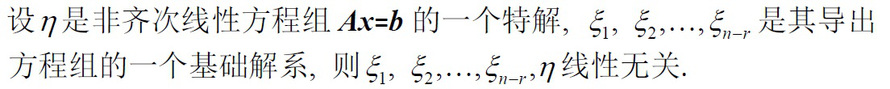
A.正确
B.错误
题目解答
答案
A. 正确
解析
步骤 1:理解非齐次线性方程组的解的结构
非齐次线性方程组 Ax=b 的解可以表示为一个特解加上其导出方程组 Ax=0 的解的线性组合。即,如果 n 是 Ax=b 的一个特解,而 ξ1, ξ2, ..., ξ_{n-1} 是 Ax=0 的一个基础解系,则 Ax=b 的通解可以表示为 n + c1ξ1 + c2ξ2 + ... + c_{n-1}ξ_{n-1},其中 c1, c2, ..., c_{n-1} 是任意常数。
步骤 2:分析线性无关性
要证明 ξ1, ξ2, ..., ξ_{n-1}, n 线性无关,我们需要证明如果存在一组常数 k1, k2, ..., k_{n-1}, k_n 使得 k1ξ1 + k2ξ2 + ... + k_{n-1}ξ_{n-1} + k_nn = 0,则 k1 = k2 = ... = k_{n-1} = k_n = 0。
步骤 3:利用导出方程组的基础解系的性质
由于 ξ1, ξ2, ..., ξ_{n-1} 是导出方程组 Ax=0 的一个基础解系,它们是线性无关的。因此,如果 k1ξ1 + k2ξ2 + ... + k_{n-1}ξ_{n-1} = 0,则 k1 = k2 = ... = k_{n-1} = 0。如果 k_nn = 0,由于 n 是非零向量(否则 n 就是导出方程组的解,而不是非齐次方程组的特解),则 k_n = 0。因此,k1 = k2 = ... = k_{n-1} = k_n = 0,这证明了 ξ1, ξ2, ..., ξ_{n-1}, n 线性无关。
非齐次线性方程组 Ax=b 的解可以表示为一个特解加上其导出方程组 Ax=0 的解的线性组合。即,如果 n 是 Ax=b 的一个特解,而 ξ1, ξ2, ..., ξ_{n-1} 是 Ax=0 的一个基础解系,则 Ax=b 的通解可以表示为 n + c1ξ1 + c2ξ2 + ... + c_{n-1}ξ_{n-1},其中 c1, c2, ..., c_{n-1} 是任意常数。
步骤 2:分析线性无关性
要证明 ξ1, ξ2, ..., ξ_{n-1}, n 线性无关,我们需要证明如果存在一组常数 k1, k2, ..., k_{n-1}, k_n 使得 k1ξ1 + k2ξ2 + ... + k_{n-1}ξ_{n-1} + k_nn = 0,则 k1 = k2 = ... = k_{n-1} = k_n = 0。
步骤 3:利用导出方程组的基础解系的性质
由于 ξ1, ξ2, ..., ξ_{n-1} 是导出方程组 Ax=0 的一个基础解系,它们是线性无关的。因此,如果 k1ξ1 + k2ξ2 + ... + k_{n-1}ξ_{n-1} = 0,则 k1 = k2 = ... = k_{n-1} = 0。如果 k_nn = 0,由于 n 是非零向量(否则 n 就是导出方程组的解,而不是非齐次方程组的特解),则 k_n = 0。因此,k1 = k2 = ... = k_{n-1} = k_n = 0,这证明了 ξ1, ξ2, ..., ξ_{n-1}, n 线性无关。