题目
求指导本题解题过程,谢谢您!3.5设随机变量X的概率密度为 f(x)= ) (e)^-x,xgt 0, 0,0thers 的分布函数及概率密度.
求指导本题解题过程,谢谢您!
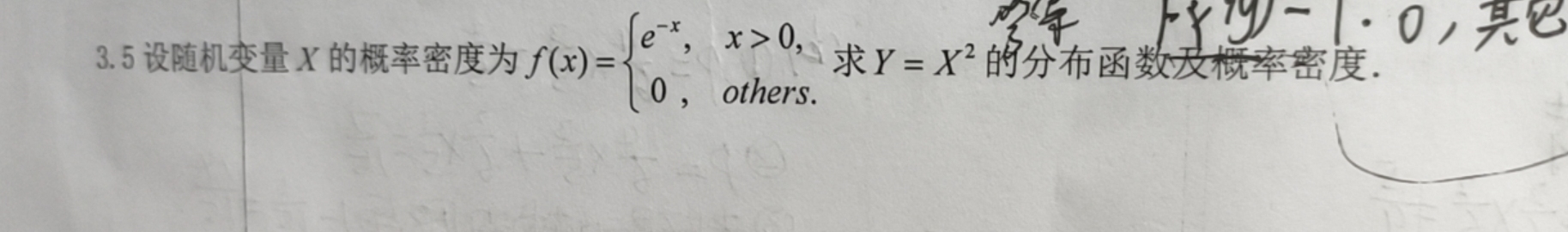
题目解答
答案

解析
步骤 1:确定 $Y$ 的分布函数
$Y = X^2$ 的分布函数 $F_Y(y)$ 定义为 $F_Y(y) = P(Y \leq y)$。由于 $Y = X^2$,我们有 $P(Y \leq y) = P(X^2 \leq y)$。根据 $X$ 的概率密度函数,$X$ 只在 $x > 0$ 时有非零概率,因此 $Y$ 也只在 $y > 0$ 时有非零概率。当 $y \leq 0$ 时,$F_Y(y) = 0$。当 $y > 0$ 时,$P(X^2 \leq y) = P(-\sqrt{y} \leq X \leq \sqrt{y})$。由于 $X$ 的概率密度函数在 $x < 0$ 时为零,我们只需考虑 $0 \leq X \leq \sqrt{y}$ 的情况,即 $P(X^2 \leq y) = P(0 \leq X \leq \sqrt{y})$。
步骤 2:计算 $F_Y(y)$
当 $y > 0$ 时,$F_Y(y) = P(0 \leq X \leq \sqrt{y}) = \int_{0}^{\sqrt{y}} f(x) dx = \int_{0}^{\sqrt{y}} e^{-x} dx$。计算这个积分,我们得到 $F_Y(y) = -e^{-x} \Big|_{0}^{\sqrt{y}} = -e^{-\sqrt{y}} + 1$。因此,$F_Y(y) = 1 - e^{-\sqrt{y}}$ 当 $y > 0$ 时。
步骤 3:确定 $Y$ 的概率密度函数
$Y$ 的概率密度函数 $f_Y(y)$ 是 $F_Y(y)$ 的导数。因此,$f_Y(y) = \frac{d}{dy} F_Y(y) = \frac{d}{dy} (1 - e^{-\sqrt{y}}) = \frac{1}{2\sqrt{y}} e^{-\sqrt{y}}$ 当 $y > 0$ 时。当 $y \leq 0$ 时,$f_Y(y) = 0$。
$Y = X^2$ 的分布函数 $F_Y(y)$ 定义为 $F_Y(y) = P(Y \leq y)$。由于 $Y = X^2$,我们有 $P(Y \leq y) = P(X^2 \leq y)$。根据 $X$ 的概率密度函数,$X$ 只在 $x > 0$ 时有非零概率,因此 $Y$ 也只在 $y > 0$ 时有非零概率。当 $y \leq 0$ 时,$F_Y(y) = 0$。当 $y > 0$ 时,$P(X^2 \leq y) = P(-\sqrt{y} \leq X \leq \sqrt{y})$。由于 $X$ 的概率密度函数在 $x < 0$ 时为零,我们只需考虑 $0 \leq X \leq \sqrt{y}$ 的情况,即 $P(X^2 \leq y) = P(0 \leq X \leq \sqrt{y})$。
步骤 2:计算 $F_Y(y)$
当 $y > 0$ 时,$F_Y(y) = P(0 \leq X \leq \sqrt{y}) = \int_{0}^{\sqrt{y}} f(x) dx = \int_{0}^{\sqrt{y}} e^{-x} dx$。计算这个积分,我们得到 $F_Y(y) = -e^{-x} \Big|_{0}^{\sqrt{y}} = -e^{-\sqrt{y}} + 1$。因此,$F_Y(y) = 1 - e^{-\sqrt{y}}$ 当 $y > 0$ 时。
步骤 3:确定 $Y$ 的概率密度函数
$Y$ 的概率密度函数 $f_Y(y)$ 是 $F_Y(y)$ 的导数。因此,$f_Y(y) = \frac{d}{dy} F_Y(y) = \frac{d}{dy} (1 - e^{-\sqrt{y}}) = \frac{1}{2\sqrt{y}} e^{-\sqrt{y}}$ 当 $y > 0$ 时。当 $y \leq 0$ 时,$f_Y(y) = 0$。