题目
4、微分方程 +xydy=(y)^2dx+ydy 的通解为-|||-A、 ^2+1=C((x-1))^2 B、 ^2-1=C(x+1)-|||-C、 ^2-1=C((x+1))^2 D、 ^2-1=C((x-1))^2
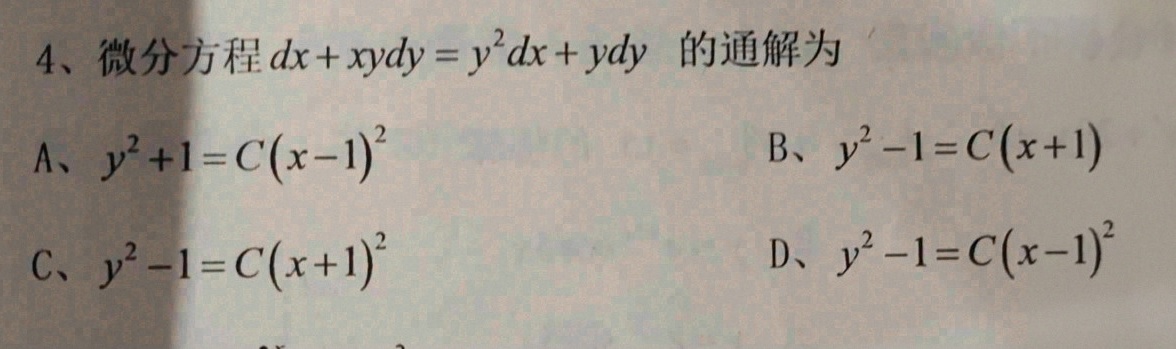
题目解答
答案

解析
步骤 1:整理方程
将方程 $dx+xydy={y}^{2}dx+ydy$ 整理为 $dx(1-{y}^{2})=dy(y-xy)$,即 $dx(1-{y}^{2})=ydy(1-x)$。
步骤 2:分离变量
将方程分离变量,得到 $\dfrac {y}{{y}^{2}-1}dy=\dfrac {1}{x-1}dx$。
步骤 3:积分
对两边积分,得到 $\dfrac {1}{2}\ln |{y}^{2}-1|=\ln |x-1|+{C}_{1}$,即 $\ln |{y}^{2}-1|=\ln {e}^{{(1-x)}^{2}}$。
步骤 4:求解
解得 ${y}^{2}-1=\pm {e}^{2{c}_{1}}{C}_{1}{(x-1)}^{2}$,即 ${y}^{2}-1=C{(x-1)}^{2}$。
将方程 $dx+xydy={y}^{2}dx+ydy$ 整理为 $dx(1-{y}^{2})=dy(y-xy)$,即 $dx(1-{y}^{2})=ydy(1-x)$。
步骤 2:分离变量
将方程分离变量,得到 $\dfrac {y}{{y}^{2}-1}dy=\dfrac {1}{x-1}dx$。
步骤 3:积分
对两边积分,得到 $\dfrac {1}{2}\ln |{y}^{2}-1|=\ln |x-1|+{C}_{1}$,即 $\ln |{y}^{2}-1|=\ln {e}^{{(1-x)}^{2}}$。
步骤 4:求解
解得 ${y}^{2}-1=\pm {e}^{2{c}_{1}}{C}_{1}{(x-1)}^{2}$,即 ${y}^{2}-1=C{(x-1)}^{2}$。