题目
求过点(2,1,3)且与直线dfrac (x+1)(3)=dfrac (y-1)(2)=dfrac (z)(-1)垂直相交的直线的方程。
求过点(2,1,3)且与直线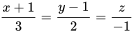
垂直相交的直线的方程。
题目解答
答案
解析
步骤 1：确定平面方程
已知直线的方向向量为 $(3, 2, -1)$，过点 $(2, 1, 3)$ 的平面垂直于该直线，因此平面的法向量为 $(3, 2, -1)$。根据点法式方程，平面方程为 $3(x-2)+2(y-1)-(z-3)=0$，即 $3x+2y-z-5=0$。
步骤 2：求直线与平面的交点
已知直线的参数方程为 $x=-1+3t$，$y=1+2t$，$z=-t$。将这些参数方程代入平面方程 $3x+2y-z-5=0$ 中，得到 $3(-1+3t)+2(1+2t)-(-t)-5=0$，即 $12t-6=0$，解得 $t=\dfrac{1}{2}$。将 $t=\dfrac{1}{2}$ 代入直线的参数方程中，得到交点坐标为 $(\dfrac{1}{2}, 2, -\dfrac{1}{2})$。
步骤 3：确定所求直线的方向向量
所求直线的方向向量为点 $(2, 1, 3)$ 到点 $(\dfrac{1}{2}, 2, -\dfrac{1}{2})$ 的向量，即 $(\dfrac{1}{2}-2, 2-1, -\dfrac{1}{2}-3) = (-\dfrac{3}{2}, 1, -\dfrac{7}{2})$。为了简化，可以取方向向量为 $(3, -2, 7)$。
步骤 4：写出所求直线的方程
所求直线的方程为 $\dfrac{x-2}{3}=\dfrac{y-1}{-2}=\dfrac{z-3}{7}$。
已知直线的方向向量为 $(3, 2, -1)$，过点 $(2, 1, 3)$ 的平面垂直于该直线，因此平面的法向量为 $(3, 2, -1)$。根据点法式方程，平面方程为 $3(x-2)+2(y-1)-(z-3)=0$，即 $3x+2y-z-5=0$。
步骤 2：求直线与平面的交点
已知直线的参数方程为 $x=-1+3t$，$y=1+2t$，$z=-t$。将这些参数方程代入平面方程 $3x+2y-z-5=0$ 中，得到 $3(-1+3t)+2(1+2t)-(-t)-5=0$，即 $12t-6=0$，解得 $t=\dfrac{1}{2}$。将 $t=\dfrac{1}{2}$ 代入直线的参数方程中，得到交点坐标为 $(\dfrac{1}{2}, 2, -\dfrac{1}{2})$。
步骤 3：确定所求直线的方向向量
所求直线的方向向量为点 $(2, 1, 3)$ 到点 $(\dfrac{1}{2}, 2, -\dfrac{1}{2})$ 的向量，即 $(\dfrac{1}{2}-2, 2-1, -\dfrac{1}{2}-3) = (-\dfrac{3}{2}, 1, -\dfrac{7}{2})$。为了简化，可以取方向向量为 $(3, -2, 7)$。
步骤 4：写出所求直线的方程
所求直线的方程为 $\dfrac{x-2}{3}=\dfrac{y-1}{-2}=\dfrac{z-3}{7}$。