题目
(6)已知随机变量X与Y相互独立,且均服从参数为λ的泊松分布,则 =x+y 服从-|||-的分布为 __

题目解答
答案
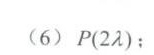
解析
考查要点:本题主要考查独立泊松分布随机变量之和的分布性质。关键在于理解泊松分布的可加性,即两个独立泊松变量相加后仍服从泊松分布,参数为原参数之和。
解题核心思路:
- 泊松分布的可加性:若$X \sim P(\lambda)$,$Y \sim P(\mu)$且独立,则$X+Y \sim P(\lambda + \mu)$。
- 验证方法:可通过卷积公式或矩母函数推导,但直接应用性质即可快速得出结论。
破题关键点:
- 明确题目中$X$和$Y$的参数均为$\lambda$,且独立,因此直接应用可加性性质,参数相加为$\lambda + \lambda = 2\lambda$。
步骤1:应用泊松分布的可加性
已知$X \sim P(\lambda)$,$Y \sim P(\lambda)$且独立,根据泊松分布的性质,独立泊松变量之和仍服从泊松分布,参数为原参数之和,即:
$Z = X + Y \sim P(\lambda + \lambda) = P(2\lambda).$
步骤2(验证):通过矩母函数推导
- 泊松分布的矩母函数为:
$M_X(t) = e^{\lambda(e^t - 1)}.$ - 因$X$和$Y$独立,$Z$的矩母函数为:
$M_Z(t) = M_X(t) \cdot M_Y(t) = e^{\lambda(e^t - 1)} \cdot e^{\lambda(e^t - 1)} = e^{2\lambda(e^t - 1)}.$ - 此结果与参数为$2\lambda$的泊松分布的矩母函数一致,故$Z \sim P(2\lambda)$。