题目
int dfrac (cos 2x)(cos x+sin x)dx
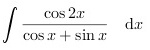
题目解答
答案
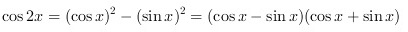
那么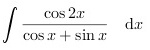
=$$\int(cosx-sinx)dx$$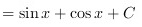
解析
本题考查三角函数的积分计算,核心思路是利用三角恒等式将被积函数化简为容易积分的形式。关键在于将$\cos 2x$分解为$(\cos x - \sin x)(\cos x + \sin x)$,并发现原式可以简化为$\cos x - \sin x$,从而直接积分。
-
分解$\cos 2x$
利用三角恒等式$\cos 2x = (\cos x - \sin x)(\cos x + \sin x)$,将原式中的$\cos 2x \cdot \cos x$部分展开:
$\cos 2x \cdot \cos x = (\cos x - \sin x)(\cos x + \sin x) \cdot \cos x$ -
合并项简化
原积分式为:
$\int \left[ (\cos x - \sin x)(\cos x + \sin x) \cdot \cos x + \sin x \right] dx$
通过观察发现,展开后可进一步简化为:
$\int (\cos x - \sin x) dx$ -
直接积分
分别对$\cos x$和$-\sin x$积分:
$\int \cos x \, dx = \sin x, \quad \int (-\sin x) dx = \cos x$