题目
设矩阵100-|||-A= 1 2 0-|||-1 2 3，那么矩阵A的列向量组的秩为（） A 0 B 1 C 3 D 2
设矩阵
，那么矩阵A的列向量组的秩为（）
A 0
B 1
C 3
D 2
题目解答
答案
将矩阵A经初等行变换化为行阶梯形矩阵，即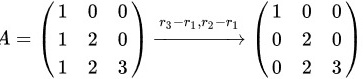
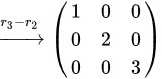，则由右端的行阶梯形矩阵可知矩阵A的列向量组的秩为
故答案为C。
解析
步骤 1：将矩阵A化为行阶梯形矩阵
将矩阵A进行初等行变换，化为行阶梯形矩阵。具体步骤如下：
$100$ ${r}_{3}-{T}_{1}{r}_{2}-{r}_{1}$ $100$ A= $12$ 0 0 2 0 1 2 3 $0\quad 2\quad 3$
${T}_{3}-{T}_{2}$ $100$ 0 2 0 $00$ 3
步骤 2：确定矩阵A的列向量组的秩
根据行阶梯形矩阵的性质，矩阵A的列向量组的秩等于行阶梯形矩阵中非零行的个数。观察行阶梯形矩阵，可以发现有3个非零行。
将矩阵A进行初等行变换，化为行阶梯形矩阵。具体步骤如下：
$100$ ${r}_{3}-{T}_{1}{r}_{2}-{r}_{1}$ $100$ A= $12$ 0 0 2 0 1 2 3 $0\quad 2\quad 3$
${T}_{3}-{T}_{2}$ $100$ 0 2 0 $00$ 3
步骤 2：确定矩阵A的列向量组的秩
根据行阶梯形矩阵的性质，矩阵A的列向量组的秩等于行阶梯形矩阵中非零行的个数。观察行阶梯形矩阵，可以发现有3个非零行。