题目
取何值时, 非齐次线性方程组有惟一解、无解或有无限多解? 并在有无限多解时求其通解.
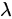 取何值时, 非齐次线性方程组
取何值时, 非齐次线性方程组
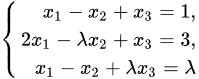
有惟一解、无解或有无限多解? 并在有无限多解时求其通解.
题目解答
答案
首先,将非齐次线性方程组转化为增广矩阵的形式:
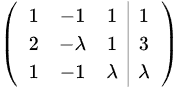
然后,对该增广矩阵进行行变换,以判断方程组的解的情况。
1. 首先,用第二行减去第一行的两倍,得到:
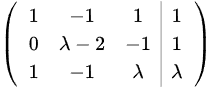
2. 接着,用第三行减去第一行,得到:
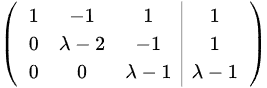
3. 现在,根据最简行阶梯形矩阵,我们可以判断方程组的解的情况:
当 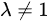 且
且 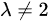 时,最简行阶梯形矩阵的第三行第三个元素不为零,因此方程组有唯一解。
时,最简行阶梯形矩阵的第三行第三个元素不为零,因此方程组有唯一解。
当 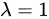 时,最简行阶梯形矩阵变为:
时,最简行阶梯形矩阵变为:
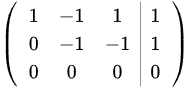
由于第三行全为零,且右边常数项列不为零,因此方程组无解。
当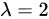 时,最简行阶梯形矩阵变为:
时,最简行阶梯形矩阵变为:

此时,方程组有无限多解。为了求出通解,我们令 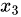 =
= 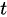 (t 为任意常数),则由最简行阶梯形矩阵可得:
(t 为任意常数),则由最简行阶梯形矩阵可得:
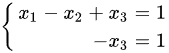
解这个方程组,得到:
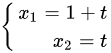
因此,当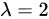 时,方程组的通解为:
时,方程组的通解为:
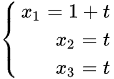
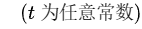
综上所述,当 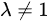 且
且 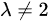 时,方程组有唯一解;当
时,方程组有唯一解;当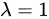 时,方程组无解;当
时,方程组无解;当 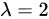 时,方程组有无限多解,通解为
时,方程组有无限多解,通解为 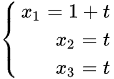 (t 为任意常数)。
(t 为任意常数)。