题目
27.设f(x)在[1,2]可导,(1,2)连续,且f(1) =2,f(2) =1,证明:(1)至少口a口(1,2),使得:f(a) =a; (2)存在两个不同的点口、口口(1,2),使得:f' (口)·f'(口)=1.
27.设f(x)在[1,2]可导,(1,2)连续,且f(1) =2,f(2) =1,证明:(1)至少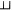 a
a (1,2),使得:f(a) =a;
(1,2),使得:f(a) =a;
(2)存在两个不同的点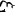 、
、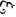
 (1,2),使得:f' (
(1,2),使得:f' (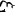 )·f'(
)·f'(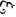 )=1.
)=1.
题目解答
答案
(1)、令F(x)=f(x)-x,x [1,2];已知f(x)在[1,2]可导,(1,2)连续,且f(1) =2,f(2) =1;可知F(1)=1
[1,2];已知f(x)在[1,2]可导,(1,2)连续,且f(1) =2,f(2) =1;可知F(1)=1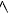 " data-width="14" data-height="15" data-size="292" data-format="png" style="max-width:100%">0,F(2)=-1
" data-width="14" data-height="15" data-size="292" data-format="png" style="max-width:100%">0,F(2)=-1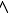 0,根据零点定理可得至少
0,根据零点定理可得至少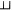 a
a (1,2),使得:F(a)=f(a) -a=0,即f(a) =a.
(1,2),使得:F(a)=f(a) -a=0,即f(a) =a.
(2)、由(1)知至少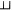 a
a (1,2),使得:f(a) =a;在[1,a],
(1,2),使得:f(a) =a;在[1,a],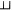 点
点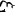
 (1,a)
(1,a)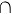 (1,2),使得f' (
(1,2),使得f' (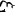 )=
)=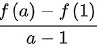 =
=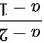 ;同样的,在[a,2],
;同样的,在[a,2],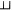 点
点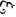
 (a,2)
(a,2)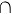 (1,2),使得f'(
(1,2),使得f'(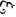 )=
)=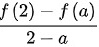 =
=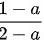 .从而有f' (
.从而有f' (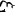 )·f'(
)·f'(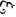 )=
)=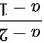 ·
·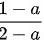 =1.即存在两个不同的点
=1.即存在两个不同的点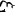 、
、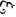
 (1,2),使得:f' (
(1,2),使得:f' (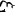 )·f'(
)·f'(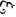 )=1,命题得证
)=1,命题得证
解析
步骤 1:定义辅助函数
定义辅助函数 $F(x) = f(x) - x$,其中 $x \in [1, 2]$。由于 $f(x)$ 在 $[1, 2]$ 上可导且在 $(1, 2)$ 上连续,因此 $F(x)$ 也在 $[1, 2]$ 上可导且在 $(1, 2)$ 上连续。
步骤 2:计算 $F(1)$ 和 $F(2)$
根据题目条件,$f(1) = 2$ 和 $f(2) = 1$,因此 $F(1) = f(1) - 1 = 2 - 1 = 1$,$F(2) = f(2) - 2 = 1 - 2 = -1$。
步骤 3:应用零点定理
由于 $F(1) = 1 > 0$,$F(2) = -1 < 0$,根据零点定理,存在 $a \in (1, 2)$,使得 $F(a) = 0$,即 $f(a) - a = 0$,从而 $f(a) = a$。
步骤 4:应用拉格朗日中值定理
在区间 $[1, a]$ 上应用拉格朗日中值定理,存在 $\xi_1 \in (1, a)$,使得 $f'(\xi_1) = \frac{f(a) - f(1)}{a - 1} = \frac{a - 2}{a - 1}$。
在区间 $[a, 2]$ 上应用拉格朗日中值定理,存在 $\xi_2 \in (a, 2)$,使得 $f'(\xi_2) = \frac{f(2) - f(a)}{2 - a} = \frac{1 - a}{2 - a}$。
步骤 5:计算 $f'(\xi_1) \cdot f'(\xi_2)$
计算 $f'(\xi_1) \cdot f'(\xi_2) = \frac{a - 2}{a - 1} \cdot \frac{1 - a}{2 - a} = 1$。
定义辅助函数 $F(x) = f(x) - x$,其中 $x \in [1, 2]$。由于 $f(x)$ 在 $[1, 2]$ 上可导且在 $(1, 2)$ 上连续,因此 $F(x)$ 也在 $[1, 2]$ 上可导且在 $(1, 2)$ 上连续。
步骤 2:计算 $F(1)$ 和 $F(2)$
根据题目条件,$f(1) = 2$ 和 $f(2) = 1$,因此 $F(1) = f(1) - 1 = 2 - 1 = 1$,$F(2) = f(2) - 2 = 1 - 2 = -1$。
步骤 3:应用零点定理
由于 $F(1) = 1 > 0$,$F(2) = -1 < 0$,根据零点定理,存在 $a \in (1, 2)$,使得 $F(a) = 0$,即 $f(a) - a = 0$,从而 $f(a) = a$。
步骤 4:应用拉格朗日中值定理
在区间 $[1, a]$ 上应用拉格朗日中值定理,存在 $\xi_1 \in (1, a)$,使得 $f'(\xi_1) = \frac{f(a) - f(1)}{a - 1} = \frac{a - 2}{a - 1}$。
在区间 $[a, 2]$ 上应用拉格朗日中值定理,存在 $\xi_2 \in (a, 2)$,使得 $f'(\xi_2) = \frac{f(2) - f(a)}{2 - a} = \frac{1 - a}{2 - a}$。
步骤 5:计算 $f'(\xi_1) \cdot f'(\xi_2)$
计算 $f'(\xi_1) \cdot f'(\xi_2) = \frac{a - 2}{a - 1} \cdot \frac{1 - a}{2 - a} = 1$。