题目
[题目]已知函数 (x-1)=(x)^2-2x, 则 f(x)= __
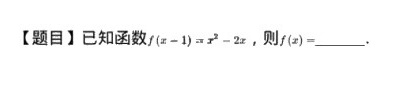
题目解答
答案

解析
步骤 1:变量替换
令 $x-1=t$,则 $x=t+1$。
步骤 2:函数表达式转换
将 $f(x-1)={x}^{2}-2x$ 转化为 $f(t)={(t+1)}^{2}-2(t+1)$。
步骤 3:化简
化简得到 $f(t)={t}^{2}-1$。
步骤 4:恢复原变量
将 $t$ 恢复为 $x$,得到 $f(x)={x}^{2}-1$。
令 $x-1=t$,则 $x=t+1$。
步骤 2:函数表达式转换
将 $f(x-1)={x}^{2}-2x$ 转化为 $f(t)={(t+1)}^{2}-2(t+1)$。
步骤 3:化简
化简得到 $f(t)={t}^{2}-1$。
步骤 4:恢复原变量
将 $t$ 恢复为 $x$,得到 $f(x)={x}^{2}-1$。