设x→0时, ^tan x-(e)^x 与x^n是同阶无穷小,则n为设x→0时, ^tan x-(e)^x 与x^n是同阶无穷小,则n为
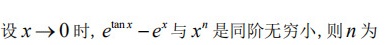

题目解答
答案
解析:
解析
考查要点:本题主要考查无穷小阶的比较,需要利用泰勒展开或等价无穷小替换来分析两个函数差的主部。
解题核心思路:
- 将$\tan x$展开为泰勒多项式,找到$\tan x - x$的主部;
- 将$e^{\tan x} - e^x$展开为泰勒多项式,通过差值运算确定最高阶项;
- 比较差值与$x^n$的阶,确定$n$的值。
破题关键点:
- 关键替换:利用$\tan x = x + \dfrac{x^3}{3} + o(x^3)$,得到$\tan x - x \sim \dfrac{x^3}{3}$;
- 指数函数展开:将$e^{\tan x} - e^x$转化为$e^x \cdot \left(e^{\tan x - x} - 1\right)$,进一步展开分析主部。
-
展开$\tan x$
当$x \to 0$时,$\tan x$的泰勒展开为:
$\tan x = x + \dfrac{x^3}{3} + o(x^3)$
因此,$\tan x - x = \dfrac{x^3}{3} + o(x^3)$,即$\tan x - x \sim \dfrac{x^3}{3}$。 -
处理指数函数差
将$e^{\tan x} - e^x$变形为:
$e^{\tan x} - e^x = e^x \cdot \left(e^{\tan x - x} - 1\right)$
由于$\tan x - x \sim \dfrac{x^3}{3}$,对$e^{\tan x - x}$展开:
$e^{\tan x - x} - 1 \approx \left(\tan x - x\right) + \dfrac{(\tan x - x)^2}{2} + \cdots$
忽略高阶小项后,主部为:
$e^{\tan x - x} - 1 \approx \dfrac{x^3}{3}$ -
确定整体阶数
代入$e^x \approx 1 + x + \dfrac{x^2}{2} + \dfrac{x^3}{6} + o(x^3)$,得:
$e^{\tan x} - e^x \approx e^x \cdot \dfrac{x^3}{3} \approx \left(1 + x + \dfrac{x^2}{2} + \dfrac{x^3}{6}\right) \cdot \dfrac{x^3}{3}$
展开后最高阶项为$\dfrac{x^3}{3}$,因此$e^{\tan x} - e^x$与$x^3$同阶。