(10)曲线 =xln (e+dfrac (1)(x))(xgt 0) 的渐近线方程为. __
题目解答
答案
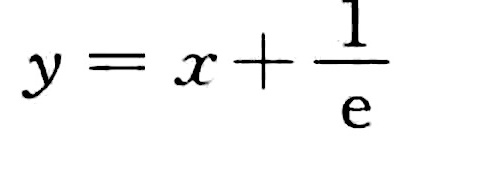
解析
考查要点:本题主要考查曲线渐近线的求解方法,特别是斜渐近线的计算。需要掌握极限的计算以及泰勒展开或等价无穷小替换的应用。
解题核心思路:
- 判断渐近线类型:当x趋向于无穷大时,若函数增长趋近于一次函数,则存在斜渐近线。
- 求斜率a:计算极限$a = \lim_{x \to \infty} \frac{y}{x}$。
- 求截距b:计算极限$b = \lim_{x \to \infty} (y - a x)$。
- 验证其他渐近线:检查x趋向于边界值时是否存在垂直渐近线。
破题关键点:
- 对数函数展开:将$\ln(e + \frac{1}{x})$展开为$1 + \frac{1}{e x} + \cdots$,简化极限计算。
- 等价无穷小替换:利用$\ln(1 + h) \approx h$(当$h \to 0$时)简化表达式。
步骤1:求斜渐近线的斜率a
计算极限:
$a = \lim_{x \to \infty} \frac{y}{x} = \lim_{x \to \infty} \ln\left(e + \frac{1}{x}\right) = \ln e = 1.$
步骤2:求斜渐近线的截距b
计算极限:
$b = \lim_{x \to \infty} \left[ x \ln\left(e + \frac{1}{x}\right) - x \right].$
令$h = \frac{1}{x}$,当$x \to \infty$时,$h \to 0$,则:
$\begin{aligned}b &= \lim_{h \to 0} \frac{\ln(e + h) - \ln e}{h} \\&= \lim_{h \to 0} \frac{\ln\left(1 + \frac{h}{e}\right)}{h} \\&= \lim_{h \to 0} \frac{\frac{h}{e}}{h} \quad (\text{等价无穷小替换}) \\&= \frac{1}{e}.\end{aligned}$
步骤3:验证垂直渐近线
当$x \to 0^+$时,$\ln(e + \frac{1}{x}) \approx \ln\left(\frac{1}{x}\right) = -\ln x$,此时:
$y = x \cdot (-\ln x) \to 0 \quad (\text{因$x \to 0$,而$-\ln x \to \infty$,但乘积趋向于0}).$
因此,无垂直渐近线。