题目
(8) int x(e)^-(x^2)dx ;
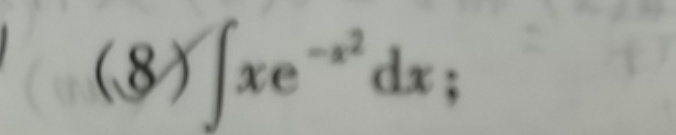
题目解答
答案

解析
考查要点:本题主要考查不定积分的计算方法,特别是凑微分法(变量代换法)的应用。
解题核心思路:
观察被积函数 $x e^{-x^2}$,发现其中存在 $x \, dx$ 与 $e^{-x^2}$ 的乘积。通过构造合适的代换变量,将积分转化为关于新变量的简单积分。关键在于识别出 $-x^2$ 的导数为 $-2x$,从而将 $x \, dx$ 转换为与新变量相关的微分形式。
破题关键点:
- 选择代换变量:令 $u = -x^2$,则 $du = -2x \, dx$,从而 $x \, dx = -\dfrac{1}{2} du$。
- 简化积分形式:将原积分转化为关于 $e^u$ 的简单积分,直接求出结果后回代变量。
步骤1:选择代换变量
令 $u = -x^2$,则微分形式为:
$du = -2x \, dx \quad \Rightarrow \quad x \, dx = -\dfrac{1}{2} du$
步骤2:代换积分变量
将原积分中的 $x \, dx$ 和 $e^{-x^2}$ 用新变量表示:
$\begin{aligned}\int x e^{-x^2} dx &= \int e^{-x^2} \cdot x \, dx \\&= \int e^{u} \cdot \left( -\dfrac{1}{2} du \right) \\&= -\dfrac{1}{2} \int e^{u} du\end{aligned}$
步骤3:计算新积分
直接对 $e^u$ 积分:
$-\dfrac{1}{2} \int e^{u} du = -\dfrac{1}{2} e^{u} + C$
步骤4:回代变量
将 $u = -x^2$ 代回,得到最终结果:
$-\dfrac{1}{2} e^{-x^2} + C$