题目
若,则一定有 ( )(A)正确(B)错误
若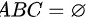 ,则一定有
,则一定有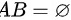 ( )
( )
(A)正确
(B)错误
题目解答
答案
若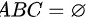 ,说明的是事件
,说明的是事件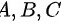 之间没有公共元素。利用韦恩图
之间没有公共元素。利用韦恩图
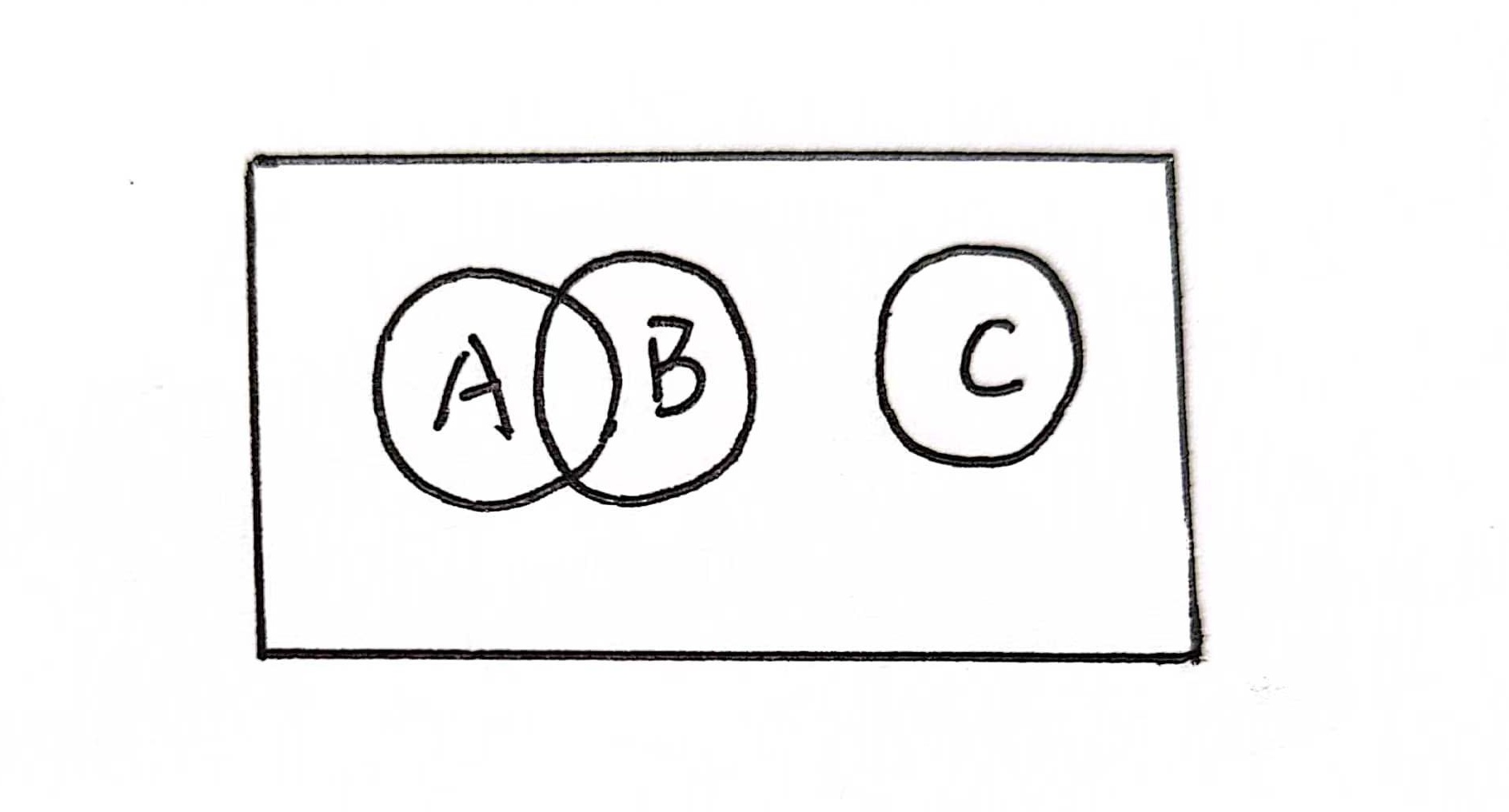
此时事件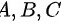 之间没有公共元素,所以有
之间没有公共元素,所以有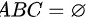 ,但此时
,但此时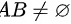 。
。
所以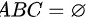 ,则不一定有
,则不一定有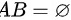
因此可以判定本题答案应该选择B选项。
解析
考查要点:本题主要考查集合的交集运算及逻辑推理能力。关键在于理解三个集合交集为空时,是否必然导致其中两个集合的交集等于某个特定集合$Q$。
解题核心思路:
- 明确符号含义:题目中的$ABC$表示三个集合的交集,即$A \cap B \cap C = \varnothing$,说明三个集合没有公共元素。
- 分析逻辑关系:题目断言“若$ABC = \varnothing$,则$AB = Q$”,需判断其是否必然成立。
- 反例验证:通过构造反例说明$ABC = \varnothing$时,$AB$可能不等于$Q$,从而推翻原命题。
破题关键点:
- 集合交集的独立性:即使三个集合无公共元素,其中两个集合的交集仍可能与第三个集合无关,从而不等于$Q$。
- 符号$Q$的不确定性:题目未定义$Q$的具体含义,因此无法直接关联$AB$与$Q$的关系。
题目逻辑分析:
- 条件分析:$ABC = \varnothing$表示$A$、$B$、$C$三者没有共同元素,但$A$和$B$的交集$AB$可能非空,只要其元素不在$C$中即可。
- 命题矛盾点:原命题认为$AB$必须等于$Q$,但$Q$未被定义,且$AB$的值由$A$和$B$本身决定,与$C$无关。
- 反例构造:
- 设$A = \{1\}$,$B = \{1\}$,$C = \{2\}$,此时$ABC = \varnothing$,但$AB = \{1\}$。
- 若$Q$为其他集合(如$\varnothing$或$\{3\}$),则$AB \neq Q$,说明原命题不成立。
结论:$ABC = \varnothing$时,$AB$不一定等于$Q$,因此原命题错误。