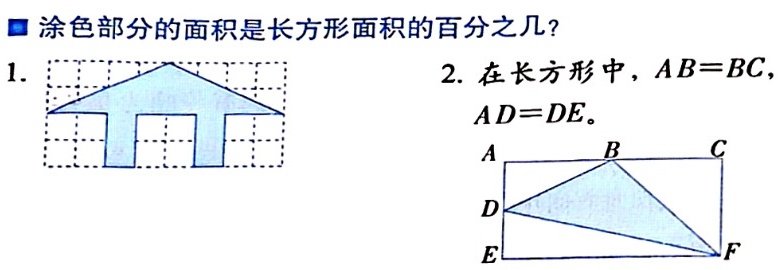
涂色部分的面积是长方形面积的百分之几?-|||-1. :-|||- -|||-2.在长方形中, AB=BC 。-|||-AD=DE ,-|||-A B C-|||-D-|||-E F

步骤 1：确定长方形的长和宽
假设长方形的长为2a，宽为2b。这样，长方形的面积为 $2a \times 2b = 4ab$。

步骤 2：计算三角形ABD的面积
由于AB=BC=a，AD=DE=b，三角形ABD的面积为 $a \times b \div 2 = \dfrac{1}{2}ab$。

步骤 3：计算三角形DEF的面积
三角形DEF的底为2a，高为b，因此面积为 $2a \times b \div 2 = ab$。

步骤 4：计算三角形BCF的面积
三角形BCF的底为a，高为2b，因此面积为 $a \times 2b \div 2 = ab$。

步骤 5：计算涂色部分的面积
涂色部分的面积为长方形的面积减去三个三角形的面积，即 $4ab - \dfrac{1}{2}ab - ab - ab = 1.5ab$。

步骤 6：计算涂色部分面积占长方形面积的百分比
涂色部分面积占长方形面积的百分比为 $1.5ab \div 4ab = 37.5\%$。