题目
[题目]-|||-若 int f(x)dx=F(x)+C, 则 int f(2x-3)dx= __ .

题目解答
答案
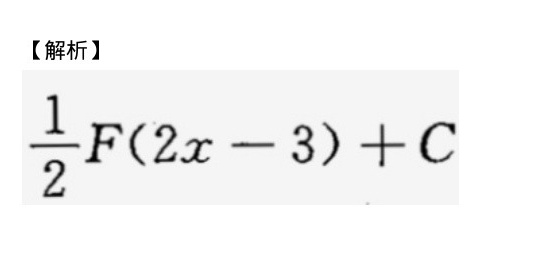
解析
步骤 1:理解积分变换
根据题目,已知 $\int f(x)dx = F(x) + C$,其中 $F(x)$ 是 $f(x)$ 的原函数,$C$ 是积分常数。现在需要求 $\int f(2x-3)dx$。
步骤 2:应用换元法
设 $u = 2x - 3$,则 $du = 2dx$,即 $dx = \frac{1}{2}du$。将 $u$ 和 $dx$ 的表达式代入原积分中,得到 $\int f(u) \cdot \frac{1}{2}du$。
步骤 3:计算积分
由于 $\int f(u)du = F(u) + C$,所以 $\int f(u) \cdot \frac{1}{2}du = \frac{1}{2}F(u) + C$。将 $u = 2x - 3$ 代回,得到 $\frac{1}{2}F(2x-3) + C$。
根据题目,已知 $\int f(x)dx = F(x) + C$,其中 $F(x)$ 是 $f(x)$ 的原函数,$C$ 是积分常数。现在需要求 $\int f(2x-3)dx$。
步骤 2:应用换元法
设 $u = 2x - 3$,则 $du = 2dx$,即 $dx = \frac{1}{2}du$。将 $u$ 和 $dx$ 的表达式代入原积分中,得到 $\int f(u) \cdot \frac{1}{2}du$。
步骤 3:计算积分
由于 $\int f(u)du = F(u) + C$,所以 $\int f(u) \cdot \frac{1}{2}du = \frac{1}{2}F(u) + C$。将 $u = 2x - 3$ 代回,得到 $\frac{1}{2}F(2x-3) + C$。