题目
设8/5在8/5二阶可导,且8/5令:8/5证明:至少8/5使得8/5
设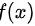 在
在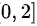 二阶可导,且
二阶可导,且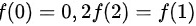 令:
令: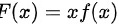 证明:至少
证明:至少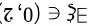 使得
使得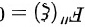
题目解答
答案
解:根据题意,我们已知函数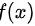 在区间
在区间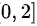 上二阶可导,且
上二阶可导,且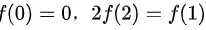 。我们要证明存在
。我们要证明存在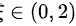 ,使得
,使得 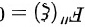 ,其中
,其中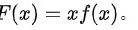
首先,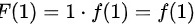
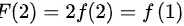
所以根据罗尔定理,如果函数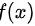 满足以下条件:在闭区间
满足以下条件:在闭区间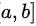 上连续,在开区间
上连续,在开区间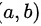 内可导,
内可导,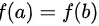 ,则至少存在一个
,则至少存在一个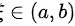 ,使得
,使得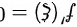
因此,由于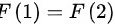 ,在
,在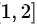 二阶可导
二阶可导
存在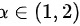 ,使得
,使得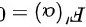
我们计算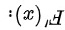
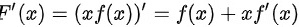
然后,计算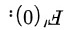
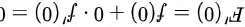
根据罗尔定理,
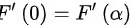 ,且在
,且在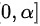 可导
可导
存在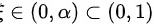 ,使得
,使得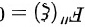
因此,我们证明了至少存在一个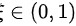 ,使得
,使得 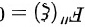 。
。
解析
步骤 1:定义函数$F(x)$
根据题目条件,我们定义$F(x)=xf(x)$,其中$f(x)$在$(0,2]$上二阶可导,且$f(0)=0$,$2f(2)=f(1)$。
步骤 2:计算$F(1)$和$F(2)$
根据定义,$F(1)=1\cdot f(1)=f(1)$,$F(2)=2\cdot f(2)=f(1)$。
步骤 3:应用罗尔定理
由于$F(1)=F(2)$,且$F(x)$在$[1,2]$上二阶可导,根据罗尔定理,存在$\alpha \in (1,2)$,使得$F'(\alpha )=$。
步骤 4:计算$F'(x)$
$F'(x)=(xf(x))'=f(x)+xf'(x)$。
步骤 5:计算$F'(0)$
$F'(0)=f(0)+0\cdot f'(0)=0$。
步骤 6:再次应用罗尔定理
由于$F'(0)=F'(\alpha )$,且$F'(x)$在$[0,\alpha ]$上可导,根据罗尔定理,存在$\xi \in (0,\alpha )\subset (0,1)$,使得$F''(\xi )=$。
根据题目条件,我们定义$F(x)=xf(x)$,其中$f(x)$在$(0,2]$上二阶可导,且$f(0)=0$,$2f(2)=f(1)$。
步骤 2:计算$F(1)$和$F(2)$
根据定义,$F(1)=1\cdot f(1)=f(1)$,$F(2)=2\cdot f(2)=f(1)$。
步骤 3:应用罗尔定理
由于$F(1)=F(2)$,且$F(x)$在$[1,2]$上二阶可导,根据罗尔定理,存在$\alpha \in (1,2)$,使得$F'(\alpha )=$。
步骤 4:计算$F'(x)$
$F'(x)=(xf(x))'=f(x)+xf'(x)$。
步骤 5:计算$F'(0)$
$F'(0)=f(0)+0\cdot f'(0)=0$。
步骤 6:再次应用罗尔定理
由于$F'(0)=F'(\alpha )$,且$F'(x)$在$[0,\alpha ]$上可导,根据罗尔定理,存在$\xi \in (0,\alpha )\subset (0,1)$,使得$F''(\xi )=$。