题目
求函数f(x,y,z)=xy+yz+zx在点P0(1,1,-2)沿方向l=(2,1,2)的方向导数.
求函数f(x,y,z)=xy+yz+zx在点P0(1,1,-2)沿方向l=(2,1,2)的方向导数.
题目解答
答案
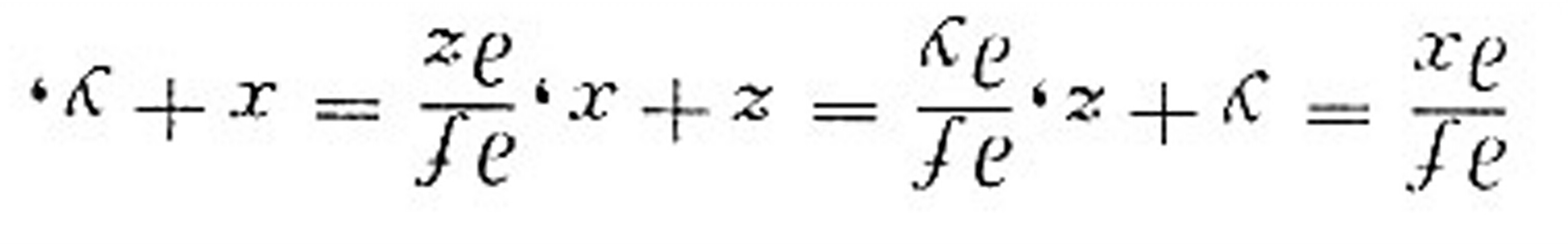
把点P0的坐标代入以上三式,得gradf(1,1,-2)=(-1,-1,2),
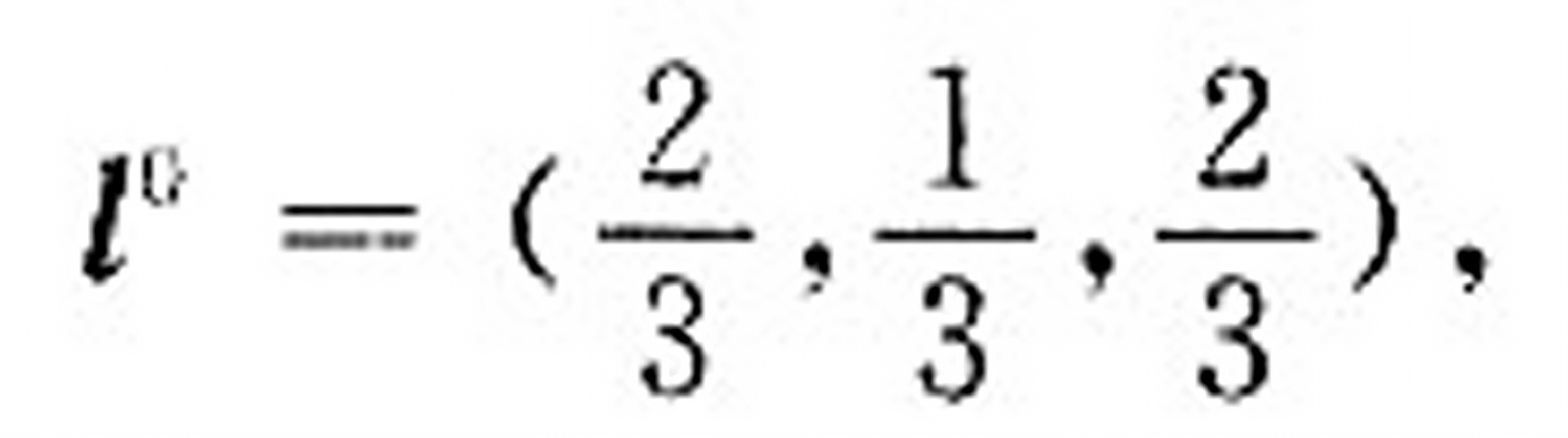
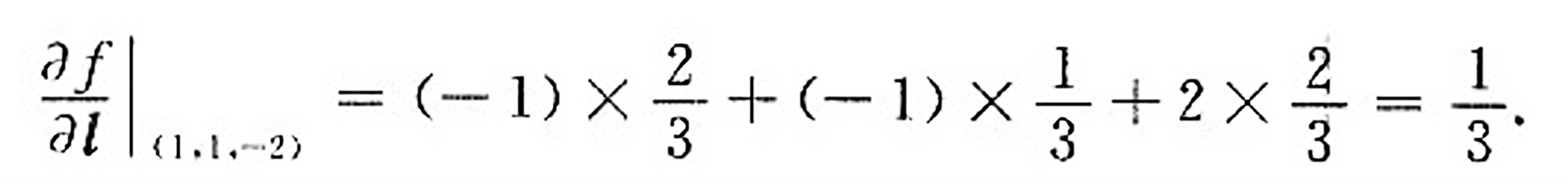
解析
步骤 1:计算函数f(x,y,z)的偏导数
计算函数f(x,y,z)=xy+yz+zx的偏导数,得到$\dfrac {\partial f}{\partial x}=y+z$,$\dfrac {\partial f}{\partial y}=z+x$,$\dfrac {\partial f}{\partial z}=x+y$。
步骤 2:计算梯度gradf(1,1,-2)
将点P_0(1,1,-2)的坐标代入偏导数,得到gradf(1,1,-2)=(-1,-1,2)。
步骤 3:计算方向l的单位向量
计算方向l=(2,1,2)的单位向量,得到$l=(\dfrac {2}{3},\dfrac {1}{3},\dfrac {2}{3})$。
步骤 4:计算方向导数
计算函数f(x,y,z)在点P_0(1,1,-2)沿方向l=(2,1,2)的方向导数,得到$\dfrac {\partial f}{\partial t}|$ ${(-1)}^{2}\times (-2)\times (-2)=(-1)\times \dfrac {1}{3}+2\times \dfrac {2}{3}=\dfrac {1}{3}$。
计算函数f(x,y,z)=xy+yz+zx的偏导数,得到$\dfrac {\partial f}{\partial x}=y+z$,$\dfrac {\partial f}{\partial y}=z+x$,$\dfrac {\partial f}{\partial z}=x+y$。
步骤 2:计算梯度gradf(1,1,-2)
将点P_0(1,1,-2)的坐标代入偏导数,得到gradf(1,1,-2)=(-1,-1,2)。
步骤 3:计算方向l的单位向量
计算方向l=(2,1,2)的单位向量,得到$l=(\dfrac {2}{3},\dfrac {1}{3},\dfrac {2}{3})$。
步骤 4:计算方向导数
计算函数f(x,y,z)在点P_0(1,1,-2)沿方向l=(2,1,2)的方向导数,得到$\dfrac {\partial f}{\partial t}|$ ${(-1)}^{2}\times (-2)\times (-2)=(-1)\times \dfrac {1}{3}+2\times \dfrac {2}{3}=\dfrac {1}{3}$。