题目
判断题:tan x)'=(sec )^2xtan x)'=(sec )^2x 正确 tan x)'=(sec )^2x 错误
判断题:
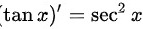
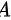 正确
正确
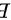 错误
错误
题目解答
答案
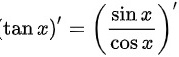
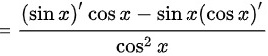
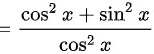
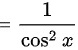
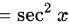
所以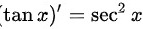 正确
正确
故本题答案为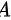
解析
步骤 1:应用商法则求导
$(\tan x)'=(\dfrac {\sin x}{\cos x})'$
步骤 2:计算分子和分母的导数
$=\dfrac {(\sin x)'\cos x-\sin x(\cos x)'}{{\cos }^{2}x}$
步骤 3:代入$\sin x$和$\cos x$的导数
$=\dfrac {{\cos }^{2}x+{\sin }^{2}x}{{\cos }^{2}x}$
步骤 4:应用三角恒等式
$=\dfrac {1}{{\cos }^{2}x}$
步骤 5:化简得到$\sec^2x$
$={\sec }^{2}x$
$(\tan x)'=(\dfrac {\sin x}{\cos x})'$
步骤 2:计算分子和分母的导数
$=\dfrac {(\sin x)'\cos x-\sin x(\cos x)'}{{\cos }^{2}x}$
步骤 3:代入$\sin x$和$\cos x$的导数
$=\dfrac {{\cos }^{2}x+{\sin }^{2}x}{{\cos }^{2}x}$
步骤 4:应用三角恒等式
$=\dfrac {1}{{\cos }^{2}x}$
步骤 5:化简得到$\sec^2x$
$={\sec }^{2}x$