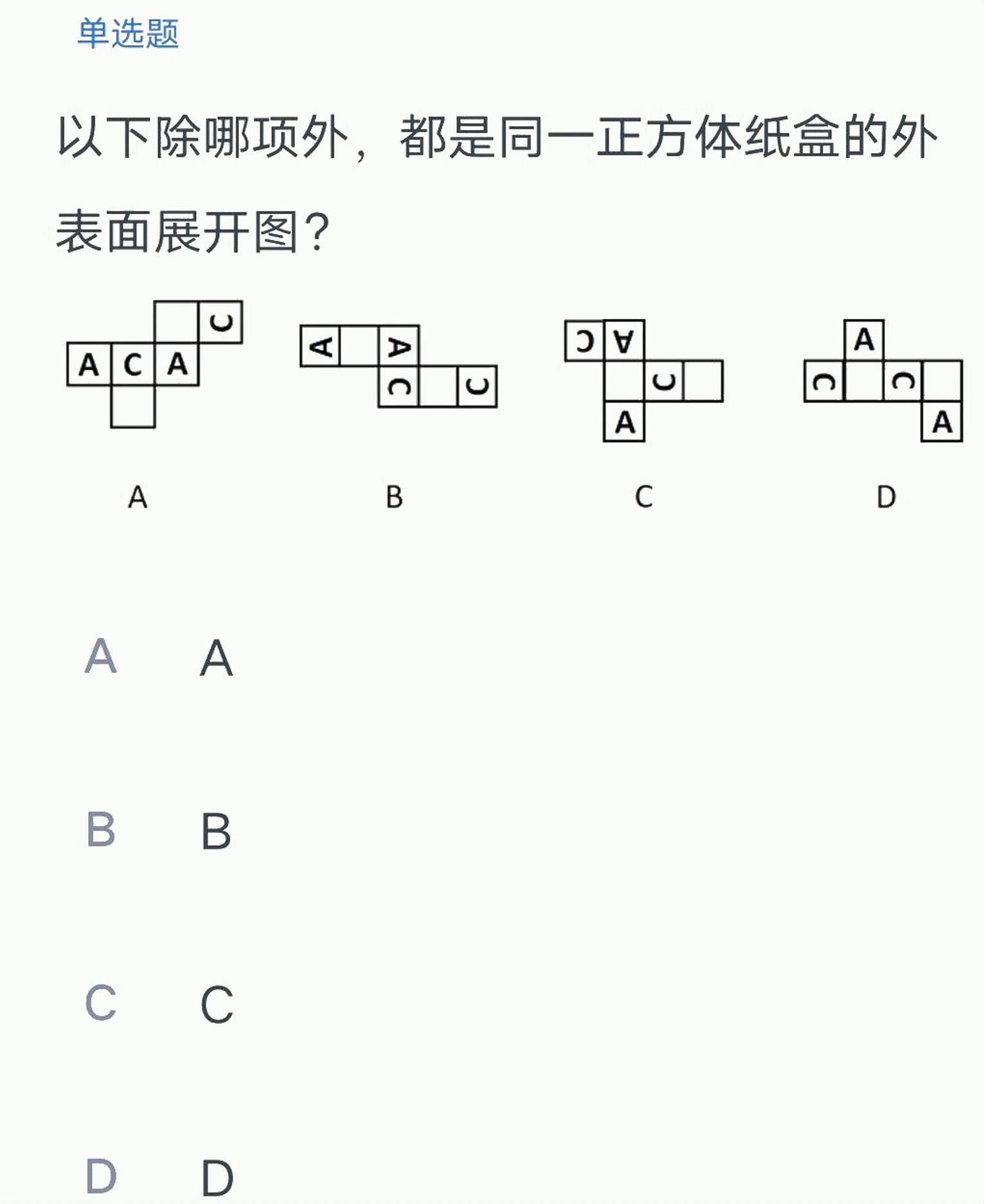
单选题-|||-以下除哪项外,都是同一正方体纸盒的外-|||-表面展开图?-|||-○ A-|||-A|C|A ○-|||-A A-|||-A B C D-|||-A A-|||-B B-|||-C C-|||-D D

考查要点：本题主要考查正方体表面展开图的识别能力，需要学生掌握正方体11种常见展开图的特征，并能判断给定图形是否属于其中一种。

解题核心思路：

1. 熟记正方体展开图的典型结构，如“141型”“231型”“33型”等。
2. 排除法：通过观察选项中图形的排列方式，判断是否存在无法折叠成立方体的结构（如出现“三连排”加“三连排”或“四连排”等错误形式）。
3. 折叠验证：若对某选项存疑，可通过想象或画图模拟折叠过程，验证是否所有面能恰好围成正方体。

破题关键点：

• 关键特征：正方体展开图中，任意一行最多连续3个正方形，且相邻行的正方形需错开排列。
• 典型错误：若某选项中存在“四个连续正方形”或“两排均三个连续正方形”，则必为错误选项。

选项分析

选项A

结构特征：中间4个正方形横向连续排列，上下各1个正方形分别与中间行的两侧正方形相连。
判断：符合“141型”展开图，可折叠成立方体。

选项B

结构特征：第一行2个正方形，第二行3个正方形，第三行1个正方形与第二行左侧相连。
判断：符合“231型”展开图，可折叠成立方体。

选项C

结构特征：上下两行各3个正方形纵向排列，且左右错开1格。
判断：符合“33型”展开图，可折叠成立方体。

选项D

结构特征：存在4个正方形连续横向排列，且剩余正方形无法与之形成有效连接。
判断：4个连续正方形的排列违反正方体展开图规则，无法折叠成立方体。