题目
求曲面 ^x-z+xy=3在点 ^x-z+xy=3处的切平面及法线方程．
求曲面
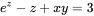在点
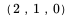处的切平面及法线方程．
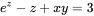在点
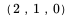处的切平面及法线方程．
题目解答
答案
由题意，设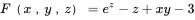
，则
曲面在点（2，1，0）处的法向量为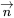
＝(Fx，Fy，Fz)|(2，1，0)
=（y，x，e z-1）| （2，1，0）=(1，2，0)
∴所求切平面方程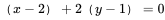 
,即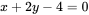
所求法线方程为:
|
|
|
解析
步骤 1：定义函数
设$F(x,y,z)={e}^{x}-z+xy-3$，则曲面在点（2，1，0）处的法向量为$\nabla F(x,y,z)$在该点的值。
步骤 2：计算梯度
计算$F(x,y,z)$的梯度$\nabla F(x,y,z) = (F_x, F_y, F_z)$，其中$F_x$，$F_y$，$F_z$分别是$F$对$x$，$y$，$z$的偏导数。
步骤 3：求偏导数
$F_x = e^x + y$，$F_y = x$，$F_z = -1$。
步骤 4：代入点(2,1,0)
将点(2,1,0)代入梯度中，得到$\nabla F(2,1,0) = (e^2 + 1, 2, -1)$。
步骤 5：求切平面方程
利用法向量$\nabla F(2,1,0)$和点(2,1,0)，写出切平面方程$(e^2 + 1)(x-2) + 2(y-1) - (z-0) = 0$。
步骤 6：化简切平面方程
化简得到切平面方程$(e^2 + 1)x + 2y - z - 2e^2 - 4 = 0$。
步骤 7：求法线方程
利用法向量$\nabla F(2,1,0)$和点(2,1,0)，写出法线方程$\frac{x-2}{e^2 + 1} = \frac{y-1}{2} = \frac{z-0}{-1}$。
设$F(x,y,z)={e}^{x}-z+xy-3$，则曲面在点（2，1，0）处的法向量为$\nabla F(x,y,z)$在该点的值。
步骤 2：计算梯度
计算$F(x,y,z)$的梯度$\nabla F(x,y,z) = (F_x, F_y, F_z)$，其中$F_x$，$F_y$，$F_z$分别是$F$对$x$，$y$，$z$的偏导数。
步骤 3：求偏导数
$F_x = e^x + y$，$F_y = x$，$F_z = -1$。
步骤 4：代入点(2,1,0)
将点(2,1,0)代入梯度中，得到$\nabla F(2,1,0) = (e^2 + 1, 2, -1)$。
步骤 5：求切平面方程
利用法向量$\nabla F(2,1,0)$和点(2,1,0)，写出切平面方程$(e^2 + 1)(x-2) + 2(y-1) - (z-0) = 0$。
步骤 6：化简切平面方程
化简得到切平面方程$(e^2 + 1)x + 2y - z - 2e^2 - 4 = 0$。
步骤 7：求法线方程
利用法向量$\nabla F(2,1,0)$和点(2,1,0)，写出法线方程$\frac{x-2}{e^2 + 1} = \frac{y-1}{2} = \frac{z-0}{-1}$。