题目
2、(1)=-1, . f(2)=2 , f(3)=1，则过这三点的二次插值多项式中(1)=-1, . f(2)=2 , f(3)=1的系数为________，拉格朗日插值多项式为(1)=-1, . f(2)=2 , f(3)=1________________________
2、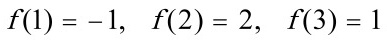
，则过这三点的二次插值多项式中
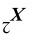的系数为________，拉格朗日插值多项式为
________________________
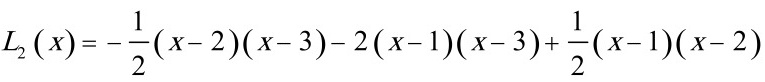题目解答
答案
-2 , 或
解析
步骤 1：确定拉格朗日插值多项式
根据题目给出的拉格朗日插值多项式${I}_{2}(x)=-\dfrac {1}{2}(x-2)(x-3)-2(x-1)(x-3)+\dfrac {1}{2}(x-1)(x-2)$，我们可以直接观察到这个多项式是二次的，因为每个因子都是线性的，且最多乘到二次项。
步骤 2：提取x^2的系数
为了找到x^2的系数，我们需要展开拉格朗日插值多项式${I}_{2}(x)$，并关注x^2项的系数。我们分别展开每个因子：
- 第一项：$-\dfrac {1}{2}(x-2)(x-3) = -\dfrac {1}{2}(x^2 - 5x + 6)$
- 第二项：$-2(x-1)(x-3) = -2(x^2 - 4x + 3)$
- 第三项：$\dfrac {1}{2}(x-1)(x-2) = \dfrac {1}{2}(x^2 - 3x + 2)$
步骤 3：合并x^2项的系数
将上述展开式合并，我们得到：
${I}_{2}(x) = -\dfrac {1}{2}x^2 + \dfrac {5}{2}x - 3 - 2x^2 + 8x - 6 + \dfrac {1}{2}x^2 - \dfrac {3}{2}x + 1$
合并同类项，得到：
${I}_{2}(x) = (-\dfrac {1}{2} - 2 + \dfrac {1}{2})x^2 + (\dfrac {5}{2} + 8 - \dfrac {3}{2})x + (-3 - 6 + 1)$
${I}_{2}(x) = -2x^2 + 8x - 8$
根据题目给出的拉格朗日插值多项式${I}_{2}(x)=-\dfrac {1}{2}(x-2)(x-3)-2(x-1)(x-3)+\dfrac {1}{2}(x-1)(x-2)$，我们可以直接观察到这个多项式是二次的，因为每个因子都是线性的，且最多乘到二次项。
步骤 2：提取x^2的系数
为了找到x^2的系数，我们需要展开拉格朗日插值多项式${I}_{2}(x)$，并关注x^2项的系数。我们分别展开每个因子：
- 第一项：$-\dfrac {1}{2}(x-2)(x-3) = -\dfrac {1}{2}(x^2 - 5x + 6)$
- 第二项：$-2(x-1)(x-3) = -2(x^2 - 4x + 3)$
- 第三项：$\dfrac {1}{2}(x-1)(x-2) = \dfrac {1}{2}(x^2 - 3x + 2)$
步骤 3：合并x^2项的系数
将上述展开式合并，我们得到：
${I}_{2}(x) = -\dfrac {1}{2}x^2 + \dfrac {5}{2}x - 3 - 2x^2 + 8x - 6 + \dfrac {1}{2}x^2 - \dfrac {3}{2}x + 1$
合并同类项，得到：
${I}_{2}(x) = (-\dfrac {1}{2} - 2 + \dfrac {1}{2})x^2 + (\dfrac {5}{2} + 8 - \dfrac {3}{2})x + (-3 - 6 + 1)$
${I}_{2}(x) = -2x^2 + 8x - 8$