求极限 lim _(xarrow 1)dfrac (ln [ cos (x-1)] )(1-sin dfrac {pi )(2)x}
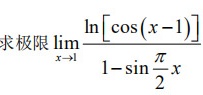
题目解答
答案
解析: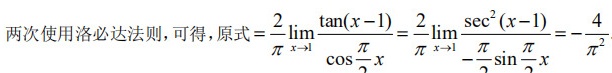
解析
考查要点:本题主要考查洛必达法则的应用,以及在处理复杂分式极限时的连续求导能力。
解题核心思路:
当直接代入$x=1$时,分子和分母均趋近于$0$,形成$\dfrac{0}{0}$型不定式,因此可以两次应用洛必达法则。每次应用时需对分子和分母分别求导,直到极限可直接计算为止。
破题关键点:
- 识别极限类型:确认为$\dfrac{0}{0}$型,满足洛必达法则的使用条件。
- 正确求导:分子和分母的导数需准确计算,尤其注意链式法则和复合函数求导。
- 符号处理:两次求导过程中负号的变化需仔细核对,避免符号错误。
步骤1:验证极限类型
当$x \rightarrow 1$时,分子$\ln[\cos(x-1)] \rightarrow \ln(1) = 0$,分母$1 - \sin\left(\dfrac{\pi}{2}x\right) \rightarrow 1 - 1 = 0$,因此为$\dfrac{0}{0}$型不定式,可应用洛必达法则。
步骤2:第一次应用洛必达法则
对分子和分母分别求导:
- 分子导数:
$\dfrac{d}{dx} \ln[\cos(x-1)] = \dfrac{1}{\cos(x-1)} \cdot (-\sin(x-1)) \cdot 1 = -\tan(x-1)$ - 分母导数:
$\dfrac{d}{dx} \left[1 - \sin\left(\dfrac{\pi}{2}x\right)\right] = -\cos\left(\dfrac{\pi}{2}x\right) \cdot \dfrac{\pi}{2}$
此时极限变为:
$\lim_{x \rightarrow 1} \dfrac{-\tan(x-1)}{-\dfrac{\pi}{2} \cos\left(\dfrac{\pi}{2}x\right)} = \lim_{x \rightarrow 1} \dfrac{\tan(x-1)}{\dfrac{\pi}{2} \cos\left(\dfrac{\pi}{2}x\right)}$
步骤3:第二次应用洛必达法则
再次代入$x=1$,分子$\tan(0)=0$,分母$\dfrac{\pi}{2} \cos\left(\dfrac{\pi}{2}\right) = 0$,仍为$\dfrac{0}{0}$型。继续求导:
- 分子导数:
$\dfrac{d}{dx} \tan(x-1) = \sec^2(x-1) \cdot 1$ - 分母导数:
$\dfrac{d}{dx} \left[\dfrac{\pi}{2} \cos\left(\dfrac{\pi}{2}x\right)\right] = \dfrac{\pi}{2} \cdot \left(-\sin\left(\dfrac{\pi}{2}x\right)\right) \cdot \dfrac{\pi}{2} = -\dfrac{\pi^2}{4} \sin\left(\dfrac{\pi}{2}x\right)$
此时极限变为:
$\lim_{x \rightarrow 1} \dfrac{\sec^2(x-1)}{-\dfrac{\pi^2}{4} \sin\left(\dfrac{\pi}{2}x\right)}$
步骤4:代入计算最终结果
当$x=1$时,$\sec^2(0) = 1$,$\sin\left(\dfrac{\pi}{2}\right) = 1$,因此:
$\lim_{x \rightarrow 1} \dfrac{1}{-\dfrac{\pi^2}{4} \cdot 1} = -\dfrac{4}{\pi^2}$