题目
2.设 =10(x)^2, 试按定义求 dfrac (dy)(dx)(|)_(x=-1).
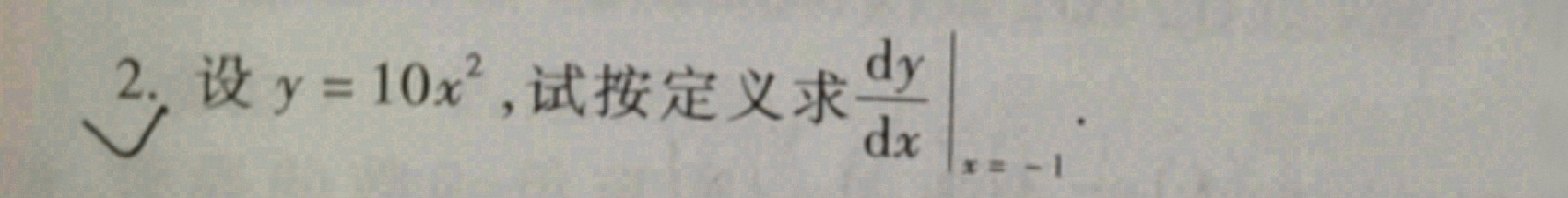
题目解答
答案

解析
本题考查导数的定义,解题思路是根据导数的定义式$\frac{dy}{dx}=\lim\limits_{\Delta x \to 0} \frac{\Delta y}{\Delta x}$来计算函数$y = 10x^2$在$x = -1$处的导数。具体步骤如下:
- 首先,根据函数$y = f(x)=10x^2$,求出$\Delta y$:
- $\Delta y=f(x+\Delta x)-f(x)$,将$x=-1$代入可得$\Delta y=f(-1 + \Delta x)-f(-1)$。
- 因为$f(-1 + \Delta x)=10(-1 + \Delta x)^2$,根据完全平方公式$(a+b)^2=a^2 + 2ab + b^2$,这里$a=-1$,$b = \Delta x$,则$f(-1 + \Delta x)=10(1 - 2\Delta x+\Delta x^2)=10 - 20\Delta x + 10\Delta x^2$。
- 又$f(-1)=10\times(-1)^2 = 10$。
- 所以$\Delta y=(10 - 20\Delta x + 10\Delta x^2)-10=-20\Delta x + 10\Delta x^2$。
- 然后,计算$\frac{\Delta y}{\Delta x}$:
- $\frac{\Delta y}{\Delta x}=\frac{-20\Delta x + 10\Delta x^2}{\Delta x}$,对分子提取公因式$\Delta x$得$\frac{\Delta y}{\Delta x}=\frac{\Delta x(-20 + 10\Delta x)}{\Delta x}$。
- 因为$\Delta x\neq0$,约分可得$\frac{\Delta y}{\Delta x}=-20 + 10\Delta x$。
- 最后,求极限$\lim\limits_{\Delta x \to 0} \frac{\Delta y}{\Delta x}$:
- $\frac{dy}{dx}\big|_{x = -1}=\lim\limits_{\Delta x \to 0} \frac{\Delta y}{\Delta x}=\lim\limits_{\Delta x \to 0}(-20 + 10\Delta x)$。
- 根据极限的运算法则$\lim\limits_{x \to a}(u(x)+v(x))=\lim\limits_{x \to a}u(x)+\lim\limits_{x \to a}v(x)$,可得$\lim\limits_{\Delta x \to 0}(-20 + 10\Delta x)=\lim\limits_{\Delta x \to 0}(-20)+\lim\limits_{\Delta x \to 0}(10\Delta x)$。
- 因为常数的极限就是其本身,所以$\lim\limits_{\Delta x \to 0}(-20)=-20$,又$\lim\limits_{\Delta x \to 0}(10\Delta x)=10\times\lim\limits_{\Delta x \to 0}\Delta x = 0$。
- 则$\frac{dy}{dx}\big|_{x = -1}=-20+0=-20$。