题目
18.求曲线 =2sqrt (x) 与直线 y=x+1 ,y=-x 所围成的图形的面积.
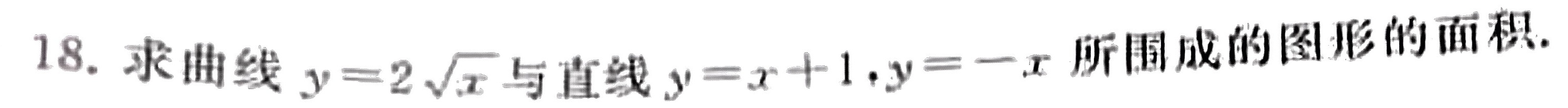
题目解答
答案
本题考查定积分的几何意义,考查学生的计算能力,属于基础题.
确定曲线交点的坐标,确定被积区间及被积函数,利用定积分表示面积,即可得到结论.
【答案】
$\dfrac{4}{3}$
【】
由$\left\{\begin{array}{l}y=2\sqrt{x}\\ y=x+1\end{array}\right.$,得$\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$,
由$\left\{\begin{array}{l}y=2\sqrt{x}\\ y=-x\end{array}\right.$,得$\left\{\begin{array}{l}x=0\\ y=0\end{array}\right.$,
由$\left\{\begin{array}{l}y=x+1\\ y=-x\end{array}\right.$,得$\left\{\begin{array}{l}x=-\frac{1}{2}\\ y=\frac{1}{2}\end{array}\right.$,
所以曲线$y=2\sqrt{x}$与直线$y=x+1$,$y=-x$所围成的形的面积为
$\int ^{1}_{0} \left ( {2\sqrt {x}+x+1} \right )dx-\int ^{0}_{-\dfrac {1} {2}} \left ( {-x+x+1} \right )dx$
$=\int ^{1}_{0} \left ( {2\sqrt {x}+x+1} \right )dx-\int ^{0}_{-\dfrac {1} {2}} {1dx}$
$=\left ( {\dfrac {4} {3}{x}^{\dfrac {3} {2}}+\dfrac {1} {2}{x}^{2}+x} \right ){|}^{1}_{0}-x{|}^{0}_{-\dfrac {1} {2}}$
$=\left ( {\dfrac {4} {3}\times {1}^{\dfrac {3} {2}}+\dfrac {1} {2}\times {1}^{2}+1} \right )-\left ( {\dfrac {4} {3}\times {0}^{\dfrac {3} {2}}+\dfrac {1} {2}\times {0}^{2}+0} \right )-\left [ {0-\left ( {-\dfrac {1} {2}} \right )} \right ]$
$=\dfrac {13} {6}-\dfrac {1} {2}=\dfrac {5} {3}$。
综上所述,结论是:曲线$y=2\sqrt{x}$与直线$y=x+1$,$y=-x$所围成的形的面积为$\dfrac{5}{3}$。
确定曲线交点的坐标,确定被积区间及被积函数,利用定积分表示面积,即可得到结论.
【答案】
$\dfrac{4}{3}$
【】
由$\left\{\begin{array}{l}y=2\sqrt{x}\\ y=x+1\end{array}\right.$,得$\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$,
由$\left\{\begin{array}{l}y=2\sqrt{x}\\ y=-x\end{array}\right.$,得$\left\{\begin{array}{l}x=0\\ y=0\end{array}\right.$,
由$\left\{\begin{array}{l}y=x+1\\ y=-x\end{array}\right.$,得$\left\{\begin{array}{l}x=-\frac{1}{2}\\ y=\frac{1}{2}\end{array}\right.$,
所以曲线$y=2\sqrt{x}$与直线$y=x+1$,$y=-x$所围成的形的面积为
$\int ^{1}_{0} \left ( {2\sqrt {x}+x+1} \right )dx-\int ^{0}_{-\dfrac {1} {2}} \left ( {-x+x+1} \right )dx$
$=\int ^{1}_{0} \left ( {2\sqrt {x}+x+1} \right )dx-\int ^{0}_{-\dfrac {1} {2}} {1dx}$
$=\left ( {\dfrac {4} {3}{x}^{\dfrac {3} {2}}+\dfrac {1} {2}{x}^{2}+x} \right ){|}^{1}_{0}-x{|}^{0}_{-\dfrac {1} {2}}$
$=\left ( {\dfrac {4} {3}\times {1}^{\dfrac {3} {2}}+\dfrac {1} {2}\times {1}^{2}+1} \right )-\left ( {\dfrac {4} {3}\times {0}^{\dfrac {3} {2}}+\dfrac {1} {2}\times {0}^{2}+0} \right )-\left [ {0-\left ( {-\dfrac {1} {2}} \right )} \right ]$
$=\dfrac {13} {6}-\dfrac {1} {2}=\dfrac {5} {3}$。
综上所述,结论是:曲线$y=2\sqrt{x}$与直线$y=x+1$,$y=-x$所围成的形的面积为$\dfrac{5}{3}$。