题目
二重积分(int )_(0)^1dx(int )_((x-1))^2f(x,y)dy,交换积分次序的结果是__________.
二重积分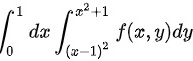
交换积分次序的结果是__________.
题目解答
答案
二重积分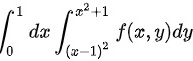先对y积分后对x积分，利用后积先定限，则x的下限为
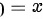，x的上限为
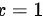，在
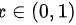区间内从下往上划条线，先交
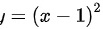为y的下限，后交
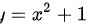为y的上限，则积分区域为
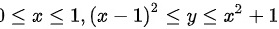，则交换积分次序，先对x积分后对y积分，则先定y的上下限，则y的下限为
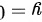，y的上限为
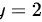，则在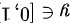
区间从左往右划条线，先交
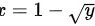为x的下限，后交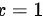为x的上限，在
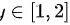区间从左往右划条线，先交
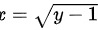为x的下限，后交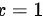为x的上限，则交换积分次序的二重积分为
.
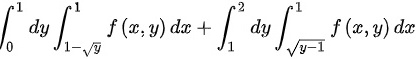解析
步骤 1：确定原积分的积分区域
原积分的积分区域由$x$的范围$0\leqslant x\leqslant 1$和$y$的范围${(x-1)}^{2}\leqslant y\leqslant {x}^{2}+1$确定。这意味着在$x$的范围内，$y$的下限是${(x-1)}^{2}$，上限是${x}^{2}+1$。
步骤 2：确定交换积分次序后的积分区域
为了交换积分次序，我们需要重新确定积分区域。在$y$的范围内，$y$的下限是$0$，上限是$2$。在$y$的范围内，从左到右划条线，先交$y={(x-1)}^{2}$为$x$的下限，后交$y={x}^{2}+1$为$x$的上限。因此，当$0\leqslant y\leqslant 1$时，$x$的下限是$1-\sqrt{y}$，上限是$1$；当$1\leqslant y\leqslant 2$时，$x$的下限是$\sqrt{y-1}$，上限是$1$。
步骤 3：写出交换积分次序后的二重积分
根据步骤2中确定的积分区域，交换积分次序后的二重积分为：
${\int }_{0}^{1}dy{\int }_{1-\sqrt{y}}^{1}f(x,y)dx+{\int }_{1}^{2}dy{\int }_{\sqrt{y-1}}^{1}f(x,y)dx$。
原积分的积分区域由$x$的范围$0\leqslant x\leqslant 1$和$y$的范围${(x-1)}^{2}\leqslant y\leqslant {x}^{2}+1$确定。这意味着在$x$的范围内，$y$的下限是${(x-1)}^{2}$，上限是${x}^{2}+1$。
步骤 2：确定交换积分次序后的积分区域
为了交换积分次序，我们需要重新确定积分区域。在$y$的范围内，$y$的下限是$0$，上限是$2$。在$y$的范围内，从左到右划条线，先交$y={(x-1)}^{2}$为$x$的下限，后交$y={x}^{2}+1$为$x$的上限。因此，当$0\leqslant y\leqslant 1$时，$x$的下限是$1-\sqrt{y}$，上限是$1$；当$1\leqslant y\leqslant 2$时，$x$的下限是$\sqrt{y-1}$，上限是$1$。
步骤 3：写出交换积分次序后的二重积分
根据步骤2中确定的积分区域，交换积分次序后的二重积分为：
${\int }_{0}^{1}dy{\int }_{1-\sqrt{y}}^{1}f(x,y)dx+{\int }_{1}^{2}dy{\int }_{\sqrt{y-1}}^{1}f(x,y)dx$。