题目
求幂级数 sum _(n=1)^infty n(n+1)(x)^n 的收敛域及和函数并求 sum _(n=1)^infty dfrac (n(n+1))({2)^n} 的和.

题目解答
答案
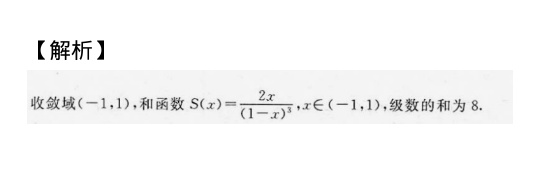
解析
步骤 1:求收敛半径
幂级数 $\sum _{n=1}^{\infty }n(n+1){x}^{n}$ 的收敛半径 $R$ 可以通过比值判别法求得。设 $a_n = n(n+1)$,则
$$
R = \lim_{n \to \infty} \left| \frac{a_n}{a_{n+1}} \right| = \lim_{n \to \infty} \left| \frac{n(n+1)}{(n+1)(n+2)} \right| = \lim_{n \to \infty} \left| \frac{n}{n+2} \right| = 1.
$$
因此,收敛半径 $R = 1$。
步骤 2:求收敛域
由于收敛半径 $R = 1$,所以幂级数在 $|x| < 1$ 时收敛。需要检查端点 $x = 1$ 和 $x = -1$ 的收敛性。
- 当 $x = 1$ 时,级数变为 $\sum _{n=1}^{\infty }n(n+1)$,这是一个发散的级数。
- 当 $x = -1$ 时,级数变为 $\sum _{n=1}^{\infty }n(n+1)(-1)^n$,这是一个发散的级数。
因此,收敛域为 $(-1, 1)$。
步骤 3:求和函数
设 $S(x) = \sum _{n=1}^{\infty }n(n+1){x}^{n}$,则
$$
S(x) = \sum _{n=1}^{\infty }n(n+1){x}^{n} = \sum _{n=1}^{\infty }n^2{x}^{n} + \sum _{n=1}^{\infty }n{x}^{n}.
$$
考虑幂级数 $\sum _{n=1}^{\infty }n{x}^{n}$ 和 $\sum _{n=1}^{\infty }n^2{x}^{n}$ 的和函数。
- 对于 $\sum _{n=1}^{\infty }n{x}^{n}$,其和函数为 $\frac{x}{(1-x)^2}$。
- 对于 $\sum _{n=1}^{\infty }n^2{x}^{n}$,其和函数为 $\frac{x(1+x)}{(1-x)^3}$。
因此,
$$
S(x) = \frac{x(1+x)}{(1-x)^3} + \frac{x}{(1-x)^2} = \frac{x(1+x) + x(1-x)}{(1-x)^3} = \frac{2x}{(1-x)^3}.
$$
所以,和函数为 $S(x) = \frac{2x}{(1-x)^3}$,$x \in (-1, 1)$。
步骤 4:求 $\sum _{n=1}^{\infty }\dfrac {n(n+1)}{{2}^{n}}$ 的和
将 $x = \frac{1}{2}$ 代入和函数 $S(x)$,得到
$$
\sum _{n=1}^{\infty }\dfrac {n(n+1)}{{2}^{n}} = S\left(\frac{1}{2}\right) = \frac{2 \cdot \frac{1}{2}}{\left(1 - \frac{1}{2}\right)^3} = \frac{1}{\left(\frac{1}{2}\right)^3} = 8.
$$
幂级数 $\sum _{n=1}^{\infty }n(n+1){x}^{n}$ 的收敛半径 $R$ 可以通过比值判别法求得。设 $a_n = n(n+1)$,则
$$
R = \lim_{n \to \infty} \left| \frac{a_n}{a_{n+1}} \right| = \lim_{n \to \infty} \left| \frac{n(n+1)}{(n+1)(n+2)} \right| = \lim_{n \to \infty} \left| \frac{n}{n+2} \right| = 1.
$$
因此,收敛半径 $R = 1$。
步骤 2:求收敛域
由于收敛半径 $R = 1$,所以幂级数在 $|x| < 1$ 时收敛。需要检查端点 $x = 1$ 和 $x = -1$ 的收敛性。
- 当 $x = 1$ 时,级数变为 $\sum _{n=1}^{\infty }n(n+1)$,这是一个发散的级数。
- 当 $x = -1$ 时,级数变为 $\sum _{n=1}^{\infty }n(n+1)(-1)^n$,这是一个发散的级数。
因此,收敛域为 $(-1, 1)$。
步骤 3:求和函数
设 $S(x) = \sum _{n=1}^{\infty }n(n+1){x}^{n}$,则
$$
S(x) = \sum _{n=1}^{\infty }n(n+1){x}^{n} = \sum _{n=1}^{\infty }n^2{x}^{n} + \sum _{n=1}^{\infty }n{x}^{n}.
$$
考虑幂级数 $\sum _{n=1}^{\infty }n{x}^{n}$ 和 $\sum _{n=1}^{\infty }n^2{x}^{n}$ 的和函数。
- 对于 $\sum _{n=1}^{\infty }n{x}^{n}$,其和函数为 $\frac{x}{(1-x)^2}$。
- 对于 $\sum _{n=1}^{\infty }n^2{x}^{n}$,其和函数为 $\frac{x(1+x)}{(1-x)^3}$。
因此,
$$
S(x) = \frac{x(1+x)}{(1-x)^3} + \frac{x}{(1-x)^2} = \frac{x(1+x) + x(1-x)}{(1-x)^3} = \frac{2x}{(1-x)^3}.
$$
所以,和函数为 $S(x) = \frac{2x}{(1-x)^3}$,$x \in (-1, 1)$。
步骤 4:求 $\sum _{n=1}^{\infty }\dfrac {n(n+1)}{{2}^{n}}$ 的和
将 $x = \frac{1}{2}$ 代入和函数 $S(x)$,得到
$$
\sum _{n=1}^{\infty }\dfrac {n(n+1)}{{2}^{n}} = S\left(\frac{1}{2}\right) = \frac{2 \cdot \frac{1}{2}}{\left(1 - \frac{1}{2}\right)^3} = \frac{1}{\left(\frac{1}{2}\right)^3} = 8.
$$