题目
(14)设 f(x)= ^2), xneq 0 0, x=0 . 试讨论f`(x)在 x=0 处的连续性.
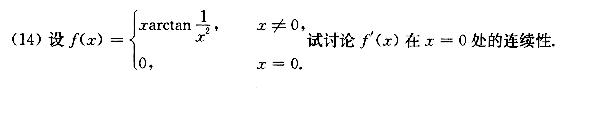
题目解答
答案
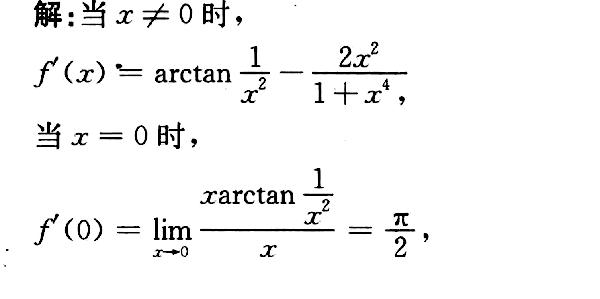

解析
步骤 1:求导
对于 $x \neq 0$,我们使用乘积法则和链式法则求导。设 $u = x$ 和 $v = \arctan \dfrac{1}{x^2}$,则 $f(x) = uv$。根据乘积法则,$f'(x) = u'v + uv'$。其中 $u' = 1$,$v' = \dfrac{d}{dx} \arctan \dfrac{1}{x^2} = \dfrac{1}{1 + \left(\dfrac{1}{x^2}\right)^2} \cdot \dfrac{d}{dx} \dfrac{1}{x^2} = \dfrac{1}{1 + \dfrac{1}{x^4}} \cdot \left(-\dfrac{2}{x^3}\right) = -\dfrac{2}{x^3 + \dfrac{1}{x}} = -\dfrac{2x^3}{x^4 + 1}$。因此,$f'(x) = \arctan \dfrac{1}{x^2} - \dfrac{2x^2}{x^4 + 1}$。
步骤 2:求导数在 x=0 处的值
当 $x = 0$ 时,我们使用导数的定义求 $f'(0)$。$f'(0) = \lim_{x \to 0} \dfrac{f(x) - f(0)}{x - 0} = \lim_{x \to 0} \dfrac{x \arctan \dfrac{1}{x^2}}{x} = \lim_{x \to 0} \arctan \dfrac{1}{x^2} = \dfrac{\pi}{2}$。
步骤 3:验证导数在 x=0 处的连续性
为了验证 $f'(x)$ 在 $x=0$ 处的连续性,我们需要检查 $\lim_{x \to 0} f'(x)$ 是否等于 $f'(0)$。$\lim_{x \to 0} f'(x) = \lim_{x \to 0} \left(\arctan \dfrac{1}{x^2} - \dfrac{2x^2}{x^4 + 1}\right) = \lim_{x \to 0} \arctan \dfrac{1}{x^2} - \lim_{x \to 0} \dfrac{2x^2}{x^4 + 1} = \dfrac{\pi}{2} - 0 = \dfrac{\pi}{2}$。因此,$\lim_{x \to 0} f'(x) = f'(0)$,所以 $f'(x)$ 在 $x=0$ 处连续。
对于 $x \neq 0$,我们使用乘积法则和链式法则求导。设 $u = x$ 和 $v = \arctan \dfrac{1}{x^2}$,则 $f(x) = uv$。根据乘积法则,$f'(x) = u'v + uv'$。其中 $u' = 1$,$v' = \dfrac{d}{dx} \arctan \dfrac{1}{x^2} = \dfrac{1}{1 + \left(\dfrac{1}{x^2}\right)^2} \cdot \dfrac{d}{dx} \dfrac{1}{x^2} = \dfrac{1}{1 + \dfrac{1}{x^4}} \cdot \left(-\dfrac{2}{x^3}\right) = -\dfrac{2}{x^3 + \dfrac{1}{x}} = -\dfrac{2x^3}{x^4 + 1}$。因此,$f'(x) = \arctan \dfrac{1}{x^2} - \dfrac{2x^2}{x^4 + 1}$。
步骤 2:求导数在 x=0 处的值
当 $x = 0$ 时,我们使用导数的定义求 $f'(0)$。$f'(0) = \lim_{x \to 0} \dfrac{f(x) - f(0)}{x - 0} = \lim_{x \to 0} \dfrac{x \arctan \dfrac{1}{x^2}}{x} = \lim_{x \to 0} \arctan \dfrac{1}{x^2} = \dfrac{\pi}{2}$。
步骤 3:验证导数在 x=0 处的连续性
为了验证 $f'(x)$ 在 $x=0$ 处的连续性,我们需要检查 $\lim_{x \to 0} f'(x)$ 是否等于 $f'(0)$。$\lim_{x \to 0} f'(x) = \lim_{x \to 0} \left(\arctan \dfrac{1}{x^2} - \dfrac{2x^2}{x^4 + 1}\right) = \lim_{x \to 0} \arctan \dfrac{1}{x^2} - \lim_{x \to 0} \dfrac{2x^2}{x^4 + 1} = \dfrac{\pi}{2} - 0 = \dfrac{\pi}{2}$。因此,$\lim_{x \to 0} f'(x) = f'(0)$,所以 $f'(x)$ 在 $x=0$ 处连续。