题目
1.函数 (x+y,xy)=(x)^2+(y)^2-xy, 则 f(x,y)=
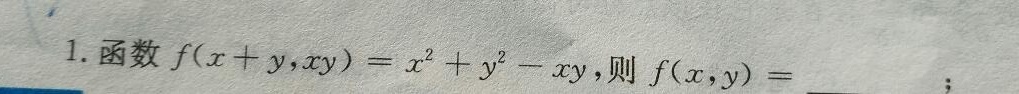
题目解答
答案
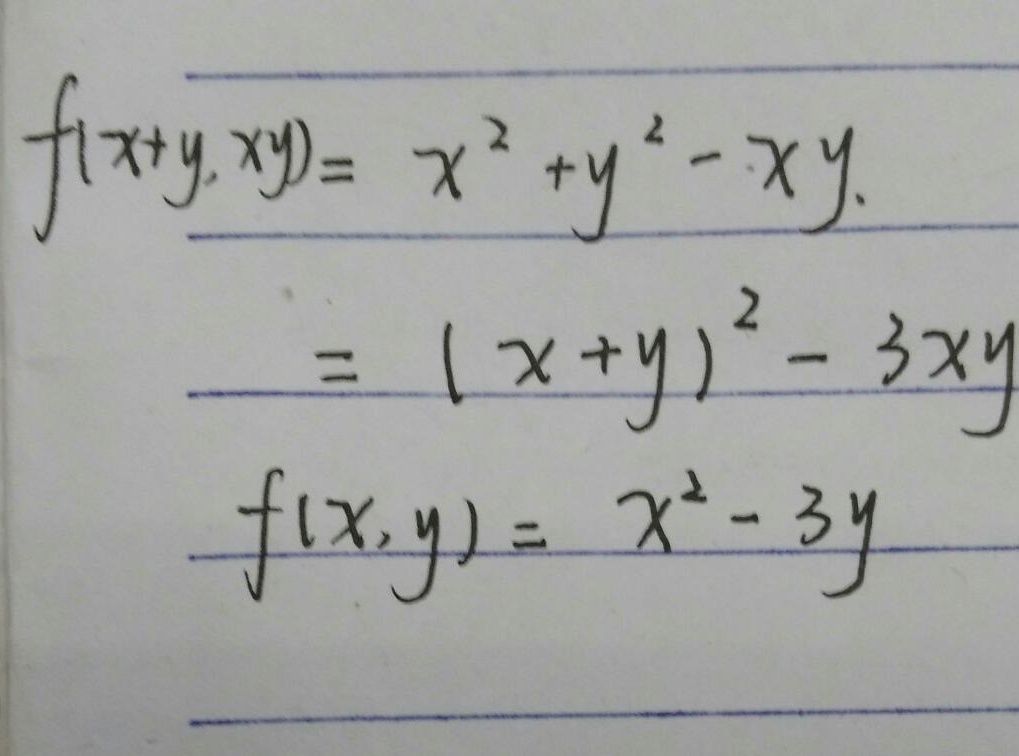
解析
步骤 1:理解函数形式
函数 $f(x+y,xy)={x}^{2}+{y}^{2}-xy$ 表示函数 $f$ 的输入是两个变量 $x+y$ 和 $xy$,输出是 ${x}^{2}+{y}^{2}-xy$。
步骤 2:将 ${x}^{2}+{y}^{2}-xy$ 用 $x+y$ 和 $xy$ 表示
我们注意到 ${x}^{2}+{y}^{2}-xy$ 可以通过代数变换用 $x+y$ 和 $xy$ 表示。首先,我们知道 ${x}^{2}+{y}^{2}={(x+y)}^{2}-2xy$,因此 ${x}^{2}+{y}^{2}-xy={(x+y)}^{2}-3xy$。
步骤 3:将 $f(x+y,xy)$ 用 $x+y$ 和 $xy$ 表示
根据步骤 2 的结果,我们可以将 $f(x+y,xy)$ 写成 $f(x+y,xy)={(x+y)}^{2}-3xy$。现在,我们用 $x$ 和 $y$ 替换 $x+y$ 和 $xy$,得到 $f(x,y)={x}^{2}-3y$。
函数 $f(x+y,xy)={x}^{2}+{y}^{2}-xy$ 表示函数 $f$ 的输入是两个变量 $x+y$ 和 $xy$,输出是 ${x}^{2}+{y}^{2}-xy$。
步骤 2:将 ${x}^{2}+{y}^{2}-xy$ 用 $x+y$ 和 $xy$ 表示
我们注意到 ${x}^{2}+{y}^{2}-xy$ 可以通过代数变换用 $x+y$ 和 $xy$ 表示。首先,我们知道 ${x}^{2}+{y}^{2}={(x+y)}^{2}-2xy$,因此 ${x}^{2}+{y}^{2}-xy={(x+y)}^{2}-3xy$。
步骤 3:将 $f(x+y,xy)$ 用 $x+y$ 和 $xy$ 表示
根据步骤 2 的结果,我们可以将 $f(x+y,xy)$ 写成 $f(x+y,xy)={(x+y)}^{2}-3xy$。现在,我们用 $x$ 和 $y$ 替换 $x+y$ 和 $xy$,得到 $f(x,y)={x}^{2}-3y$。