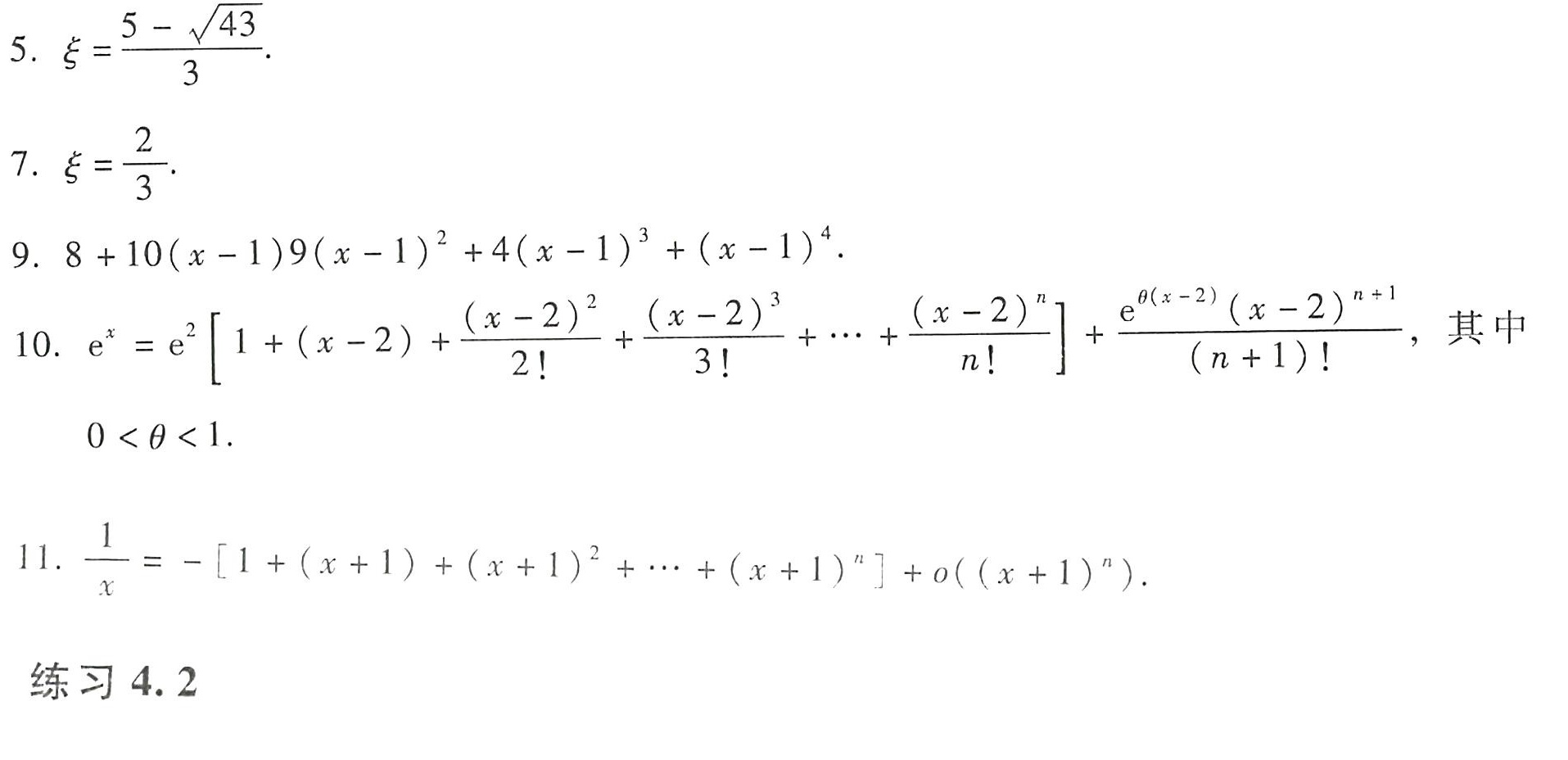5.验证函数 (x)=(x)^3-5(x)^2+x-2 在区间 [ -1,0] 上满足拉格朗日中值定理的条件,-|||-并求出结论中相应的ξ-|||-6.证明下列不等式:-|||-(1) |arctan a-arctan b|leqslant |a-b| ;-|||-(2)当 gt 1 时, ^xgt ecdot x ;-|||-(3)当 gt 0 时, ln (1+dfrac (1)(x))gt dfrac (1)(1+x)-|||-7.证明:当 geqslant 1 时,有 arctan x+arccos dfrac (2x)(1+{x)^2}=pi .-|||-8.验证函数 (x)=(x)^3 及 (x)=(x)^2+1 在区间[0,1]上满足柯西中值定理的条件,并-|||-求出结论中相应的ξ.-|||-9.按 x-1 的幂展开多项式 (x)=(x)^4+3(x)^2+4 。-|||-10.求函数 (x)=(e)^x 在点 x=2 处带拉格朗日型余项的n阶泰勒公式.-|||-11.将函数 (x)=dfrac (1)(x) 按 x+1 的幂展开,求其带佩亚诺型余项的n阶泰勒公式.-|||-S 4.2未定式的定值 ---洛必达(L '+Hospital )法则-|||-观察下列分式的极限:-|||-当x→0时,分式的分子、分母都趋于0,而分式的极限可能存在,也可能不-|||-.lim _(xarrow 0)dfrac (sin x)(x) ,lim _(xarrow 0)dfrac (sin x)({x)^2} lim _(xarrow 0)dfrac (sin xcos dfrac {1)(x)}(x) .-|||-存在,所以称它们为" dfrac (0)(0) 型"的未定式.同样的情况也发生在分子、分母的-|||-极限是∞的情形,这时称为" dfrac (alpha )(alpha ) 型"的未定式.这两种未定式统称为基本型-|||-未定式.借助于微分中值定理,可以利用导数来计算基本型未定式的极限,这-|||-就是所谓的洛必达法则.