题目
[例9]设f(x)在[0,1]上连续, (0)=0, (int )_(0)^1f(x)dx=0.-|||-求证:存在 xi in (0,1), 使 (int )_(0)^pi f(x)dx=xi f(xi ).
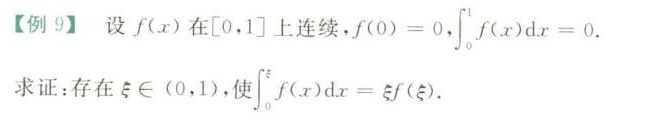
题目解答
答案

解析
步骤 1:定义辅助函数
定义辅助函数 $F(x)$ 如下:
$$
F(x) = \left \{ \begin{matrix}
\dfrac {{\int }_{0}^{x}f(t)dt}{x}, & 0\lt x\leqslant 1\\
0, & x=0.
\end{matrix} \right.
$$
步骤 2:验证 $F(x)$ 在 $[0,1]$ 上连续
由于 $f(x)$ 在 $[0,1]$ 上连续,且 $f(0)=0$,则 $F(x)$ 在 $(0,1]$ 上连续。同时,$F(x)$ 在 $x=0$ 处的极限为:
$$
\lim _{x\rightarrow {0}^{+}}F(x)=\lim _{x\rightarrow {0}^{+}}\dfrac {{\int }_{0}^{x}f(t)dt}{x}=\lim _{x\rightarrow {0}^{+}}\dfrac {f(x)}{1}=0
$$
因此,$F(x)$ 在 $[0,1]$ 上连续。
步骤 3:应用罗尔定理
由于 $F(0)=F(1)=0$,则 $F(x)$ 在 $[0,1]$ 上满足罗尔定理条件。因此,存在 $\xi \in (0,1)$,使得 $F'(\xi)=0$。
步骤 4:计算 $F'(\xi)$
$$
F'(\xi) = -\xi f(\xi) - \int_{0}^{\xi} f(t)dt = 0
$$
步骤 5:得到结论
由步骤 4 可得:
$$
\int_{0}^{\xi} f(x)dx = \xi f(\xi)
$$
定义辅助函数 $F(x)$ 如下:
$$
F(x) = \left \{ \begin{matrix}
\dfrac {{\int }_{0}^{x}f(t)dt}{x}, & 0\lt x\leqslant 1\\
0, & x=0.
\end{matrix} \right.
$$
步骤 2:验证 $F(x)$ 在 $[0,1]$ 上连续
由于 $f(x)$ 在 $[0,1]$ 上连续,且 $f(0)=0$,则 $F(x)$ 在 $(0,1]$ 上连续。同时,$F(x)$ 在 $x=0$ 处的极限为:
$$
\lim _{x\rightarrow {0}^{+}}F(x)=\lim _{x\rightarrow {0}^{+}}\dfrac {{\int }_{0}^{x}f(t)dt}{x}=\lim _{x\rightarrow {0}^{+}}\dfrac {f(x)}{1}=0
$$
因此,$F(x)$ 在 $[0,1]$ 上连续。
步骤 3:应用罗尔定理
由于 $F(0)=F(1)=0$,则 $F(x)$ 在 $[0,1]$ 上满足罗尔定理条件。因此,存在 $\xi \in (0,1)$,使得 $F'(\xi)=0$。
步骤 4:计算 $F'(\xi)$
$$
F'(\xi) = -\xi f(\xi) - \int_{0}^{\xi} f(t)dt = 0
$$
步骤 5:得到结论
由步骤 4 可得:
$$
\int_{0}^{\xi} f(x)dx = \xi f(\xi)
$$