题目
求极限__-|||-lim _(narrow infty )dfrac (n)(ln n)(sqrt [n](n)-1).
求极限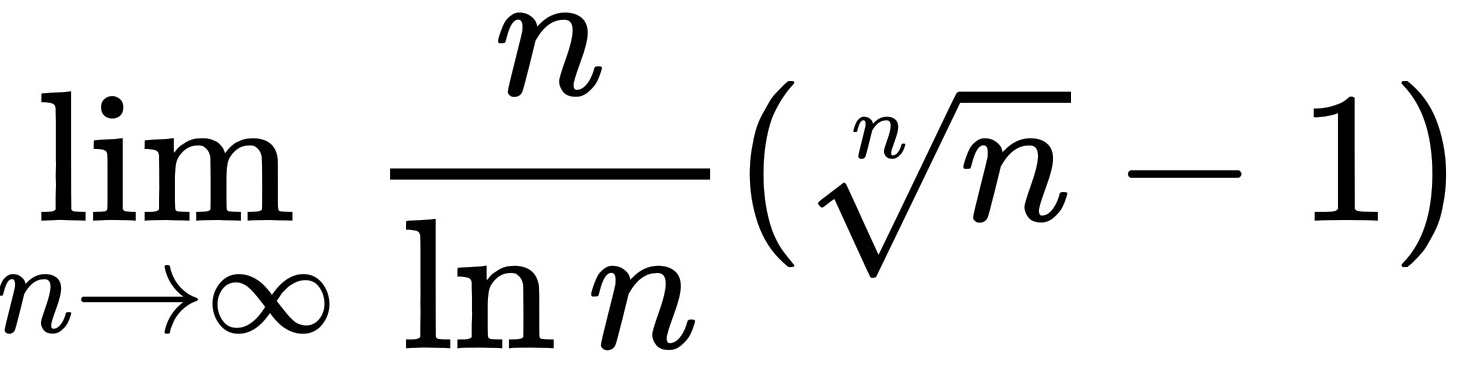 .
.
题目解答
答案
因为 ,
,
故当 时,
时,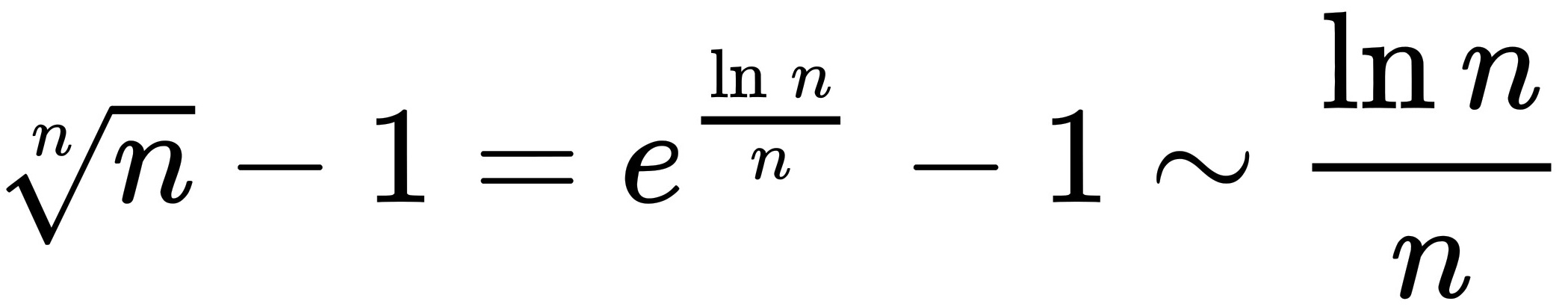 ,
,
因此,
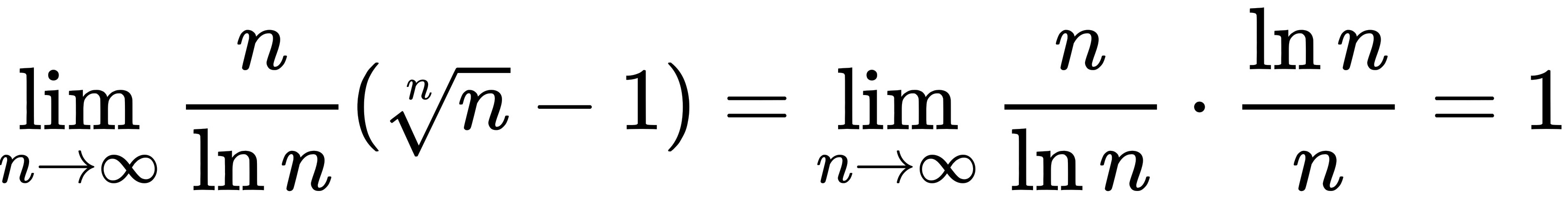 .
.
解析
步骤 1:应用洛必达法则
首先,我们注意到当$n$趋向于无穷大时,$\ln n$和$n$都趋向于无穷大,因此$\dfrac{\ln n}{n}$是一个$\frac{\infty}{\infty}$型的极限。我们可以应用洛必达法则来求解这个极限。洛必达法则指出,如果$\lim_{n\to\infty}f(n)=\lim_{n\to\infty}g(n)=\infty$,且$\lim_{n\to\infty}\frac{f'(n)}{g'(n)}$存在,则$\lim_{n\to\infty}\frac{f(n)}{g(n)}=\lim_{n\to\infty}\frac{f'(n)}{g'(n)}$。对于$\dfrac{\ln n}{n}$,我们有$f(n)=\ln n$和$g(n)=n$,因此$f'(n)=\frac{1}{n}$和$g'(n)=1$。应用洛必达法则,我们得到$\lim_{n\to\infty}\dfrac{\ln n}{n}=\lim_{n\to\infty}\dfrac{\frac{1}{n}}{1}=\lim_{n\to\infty}\dfrac{1}{n}=0$。
步骤 2:利用等价无穷小
由于$\lim_{n\to\infty}\dfrac{\ln n}{n}=0$,我们可以利用等价无穷小的概念,即当$n$趋向于无穷大时,$\sqrt[n]{n}-1$可以近似为$\dfrac{\ln n}{n}$。这是因为$\sqrt[n]{n}=e^{\frac{\ln n}{n}}$,而当$x$趋向于0时,$e^x-1\sim x$。因此,当$n$趋向于无穷大时,$\sqrt[n]{n}-1\sim \dfrac{\ln n}{n}$。
步骤 3:计算极限
现在,我们来计算原极限$\lim_{n\to\infty}\dfrac{n}{\ln n}(\sqrt[n]{n}-1)$。根据步骤2,我们可以将$\sqrt[n]{n}-1$替换为$\dfrac{\ln n}{n}$,因此原极限变为$\lim_{n\to\infty}\dfrac{n}{\ln n}\cdot\dfrac{\ln n}{n}=\lim_{n\to\infty}1=1$。
首先,我们注意到当$n$趋向于无穷大时,$\ln n$和$n$都趋向于无穷大,因此$\dfrac{\ln n}{n}$是一个$\frac{\infty}{\infty}$型的极限。我们可以应用洛必达法则来求解这个极限。洛必达法则指出,如果$\lim_{n\to\infty}f(n)=\lim_{n\to\infty}g(n)=\infty$,且$\lim_{n\to\infty}\frac{f'(n)}{g'(n)}$存在,则$\lim_{n\to\infty}\frac{f(n)}{g(n)}=\lim_{n\to\infty}\frac{f'(n)}{g'(n)}$。对于$\dfrac{\ln n}{n}$,我们有$f(n)=\ln n$和$g(n)=n$,因此$f'(n)=\frac{1}{n}$和$g'(n)=1$。应用洛必达法则,我们得到$\lim_{n\to\infty}\dfrac{\ln n}{n}=\lim_{n\to\infty}\dfrac{\frac{1}{n}}{1}=\lim_{n\to\infty}\dfrac{1}{n}=0$。
步骤 2:利用等价无穷小
由于$\lim_{n\to\infty}\dfrac{\ln n}{n}=0$,我们可以利用等价无穷小的概念,即当$n$趋向于无穷大时,$\sqrt[n]{n}-1$可以近似为$\dfrac{\ln n}{n}$。这是因为$\sqrt[n]{n}=e^{\frac{\ln n}{n}}$,而当$x$趋向于0时,$e^x-1\sim x$。因此,当$n$趋向于无穷大时,$\sqrt[n]{n}-1\sim \dfrac{\ln n}{n}$。
步骤 3:计算极限
现在,我们来计算原极限$\lim_{n\to\infty}\dfrac{n}{\ln n}(\sqrt[n]{n}-1)$。根据步骤2,我们可以将$\sqrt[n]{n}-1$替换为$\dfrac{\ln n}{n}$,因此原极限变为$\lim_{n\to\infty}\dfrac{n}{\ln n}\cdot\dfrac{\ln n}{n}=\lim_{n\to\infty}1=1$。