题目
曲线=(2x+1)arcsin x的斜渐近线为______.
曲线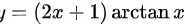
的斜渐近线为______.
题目解答
答案
对于曲线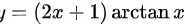，其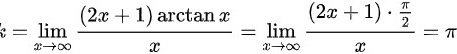
，
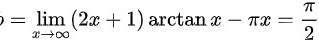，利用函数斜渐近线定义，曲线斜渐近线为
.
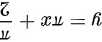故答案为：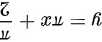
解析
步骤 1：计算斜率
计算斜率$k$，即$\lim _{x\rightarrow \infty }\dfrac {y}{x}=\lim _{x\rightarrow \infty }\dfrac {(2x+1)\arctan x}{x}$。由于$\arctan x$在$x\rightarrow \infty$时趋近于$\dfrac{\pi}{2}$，所以$k=\lim _{x\rightarrow \infty }\dfrac {(2x+1)\cdot \dfrac {\pi}{2}}{x}=\pi$。
步骤 2：计算截距
计算截距$b$，即$\lim _{x\rightarrow \infty }(y-kx)=\lim _{x\rightarrow \infty }((2x+1)\arctan x-\pi x)$。由于$\arctan x$在$x\rightarrow \infty$时趋近于$\dfrac{\pi}{2}$，所以$b=\lim _{x\rightarrow \infty }((2x+1)\cdot \dfrac {\pi}{2}-\pi x)=\dfrac {\pi }{2}$。
步骤 3：写出斜渐近线方程
根据斜率$k$和截距$b$，写出斜渐近线方程$y=kx+b$，即$y=\pi x+\dfrac {\pi }{2}$。
计算斜率$k$，即$\lim _{x\rightarrow \infty }\dfrac {y}{x}=\lim _{x\rightarrow \infty }\dfrac {(2x+1)\arctan x}{x}$。由于$\arctan x$在$x\rightarrow \infty$时趋近于$\dfrac{\pi}{2}$，所以$k=\lim _{x\rightarrow \infty }\dfrac {(2x+1)\cdot \dfrac {\pi}{2}}{x}=\pi$。
步骤 2：计算截距
计算截距$b$，即$\lim _{x\rightarrow \infty }(y-kx)=\lim _{x\rightarrow \infty }((2x+1)\arctan x-\pi x)$。由于$\arctan x$在$x\rightarrow \infty$时趋近于$\dfrac{\pi}{2}$，所以$b=\lim _{x\rightarrow \infty }((2x+1)\cdot \dfrac {\pi}{2}-\pi x)=\dfrac {\pi }{2}$。
步骤 3：写出斜渐近线方程
根据斜率$k$和截距$b$，写出斜渐近线方程$y=kx+b$，即$y=\pi x+\dfrac {\pi }{2}$。